Đáp án B

Cách 1:

Dùng chức năng lập bảng của máy tính (MODE7 TABLE)

+ Tìm hàm biến này theo biến kia k 2  theo biến  k 1 qua điều kiện trùng nhau:

x 1 = x 2 ⇔ k 1 λ 1 = k 2 + 0 , 5 λ 2 ⇒ k 2 = 5 4 k 1 − 1 2 1

+ Tìm giới hạn của biến  k 1  dựa vào vùng MN:

1 , 5 m m ≤ x 1 ≤ 9 , 5 m m ⇔ 1 , 5 m m ≤ k 1 0 , 5.2 2 ≤ 9 , 5 m m ⇔ 3 ≤ k 1 ≤ 19    2

Bấm máy:    MODE7 nhập  f x = 5 4 x − 1 2  theo phương trình (1)

Bấm = nhập giá trị của k 1  theo phương trình (2)

Start? Nhập 3

End? Nhập 19

Step? Nhập 1 (vì giá trị  k 1 ;   k 2 nguyên)

Bấm = ta được bảng giá trị  k 1 ;   k 2  ta lấy các cặp giá trị nguyên

Cách 2:Như vậy có 4 cặp giá trị ( k 1 ;   k 2 ) nguyên. Như vậy trên MN có 4 vân sáng của bức xạ  λ 1  trùng với vân tối của bức xạ  λ 2 . Chọn B

Điều kiện để trùng nhau là:  x 1 = x 2

k 1 λ 1 = k 2 + 0 , 5 λ 2 ⇒ k 1 k 2 + 0 , 5 = λ 2 λ 1 = 2 2 , 5 = 6 7 , 5 = 10 12 , 5 = ...

+ Khoảng cách ngắn nhất giữa 2 VT trùng nhau của vân tối bức xạ  λ 2  với vân sáng của bức xạ  λ 1 là:  i t r = 4 i 1 = 2 m m

+ Bắt đầu trùng nhau từ vân sáng bậc 2 của  λ 1

⇒  Vị trí trùng nhau:  x = 2 i 1 + k . i t r = 1 + 2. k

1 , 5 ≤ x = 1 + 2. k ≤ 9 , 5 ⇒ 0 , 25 ≤ k ≤ 4 , 25 ⇒ k = 1 , 2 , 3 , 4 ⇒ có 4 vân tối của bức xạ  λ 1  trùng với vân sáng bức xạ  λ 2  trên MN. Chọn B

Cách 3:

Khoảng vân:  i 1 = λ 1 D a = 0 , 5 m m ;   i 2 = λ 2 D a = 0 , 4 m m

Tại vị trí vân sáng của bức xạ  λ 1  trùng với vân tối của bức xạ  λ 2 ta có:

x = k 1 i 1 = 2 k 2 + 1 i 2 2 ⇔ 5 k 1 = 2 2 k 2 + 1 ⇒ k 1 = 2 n 2 k 2 + 1 = 5 2 n + 1 ⇒ x = 5 2 n + 1 i 2 2 = 2 n + 1 m m 1

Với  1 , 5 m m ≤ x ≤ 9 , 5 m m    2

Từ (1) và (2) suy ra:  0 , 25 ≤ n ≤ 4 , 25

Chọn: 1, 2, 3, 4  ⇒  có 4 vân tối của bức xạ  λ 1  trùng với vân sáng của bức xạ  λ 2  trên MN

Chọn C.

Đáp án C

Khi vân sang của bức xạ  λ 1  trùng với vân tối của bức xạ  λ 2

k 1 k 2 + 0 , 5 = λ 2 λ 1 = 2 2 , 5 = 6 7 , 5 = ... i 2 = λ 2 D a = 0 , 75   m m

Trên đoạn MN có 4 vị trí vân sáng của bức xạ  λ 1  trùng với vân tối của bức xạ  λ 2

Đáp án D

Phương pháp: Công thức xác định vị trí vân tối  x t = k + 1 2 λ D a

Cách giải: Ta có:

Mà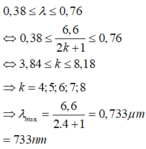 

Chọn đáp án B.

Từ vân sáng bậc 1 đến vân sáng bậc 13 của bức xạ A có 3 vân trùng thì các vân trùng đó chính là các vân trùng bậc 4, bậc 8 và bậc 12 của bức xạ A (bước nhảy 4).

Tại vị trí vân sáng bậc 4 của bức xạ λ_A có:

Với 380 nm ≤  λ ≤ 760 nm ta có: 6,3 ≤  k < 3,2  => có 3 giá trị của k thỏa mãn k thuộc Z là 4; 5 và 6;

k = 4 là vân sáng bậc 4 của bức xạ λ_A;

k = 5 thì 

k = 6 thì ; 400 không có trong các lựa chọn nên chọn 390 (nm).

ĐÁP ÁN C.

Đáp án C

Gọi 3 vân trùng này tương ứng với 3 vân của A : vân thứ x, vân thứ x + m và vân thứ x + 2m. Để ý thấy trung tâm O cũng là 1 vân trùng => 0 + m = x hay x = m. Suy ra các vân trung là vân m, vân 2m và vân 3m. Hiển nhiên có 3 m ≤ 13 . Để chỉ có 3 vị trí trùng thì vân 4m phải nằm ngoài vân 13, tức là 4m > 13. Từ đó tìm được m = 4, các vân trùng là 4, 8, 12.

Đáp án D

Phương pháp: Coi sự giao thoa trùng vân giống như giao thoa ánh sáng đơn sắc, ta đi tìm khoảng vân trùng nhau.

Cách giải:

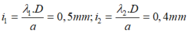
Vị trí vân sáng và vân tối thỏa mãn điều kiện : 

Vì vân sáng trùng với vị trí vân tối nên ta có: 

Coi đây là hiện tượng giao thoa với khoảng vân trùng nhau là: 

Số vân trùng nhau trong khoảng MN thỏa mãn điều kiện :

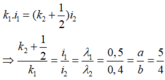
=> k = 3,4,5,6,7,8,9,10,11,12,13,14,15,16,17

Vậy có 15 giá trị k thỏa mãn