Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : \(i=\frac{D\lambda}{a}\)
vị trí vân tối là \(x=i\left(k+\frac{1}{2}\right)\)
Khi vân tối đấu tiên có nghĩa là vị trí mà 3 vân tối trùng nhau
Vì là vị trí vân tối số 14 của bước sóng 3 nên
\(x=13.5i_3\)
Mặt khác: \(x=\left(m+0.5\right)i_1=\left(n+0.5\right)i_2=13.5i_3\)
\(\left(m+0.5\right)\lambda_1=\left(n+0.5\right)\lambda_2=13.5\lambda_3\)
Mà: \(400nm<\lambda_3<760nm\)
Suy ra: 10 < n < 19
Để bước sóng 1 và 2 cùng tối và n trong khoảng đã xét mà tỉ lệ 2 bước sóng là 7:9
có các nghiệm nguyên của n là 10,17 khi đó m là 13 và 22
loại nghiệm 10 ta được n=17
\(\Rightarrow\lambda_3=700nm\)
Vị trí sáng trùng của 2 bước sóng là
\(y=k.i_2=p.i_3\)
vị trí đầu tiên này là cực đại thứ 35 của bước sóng 2 và là cực đại 27 của bước sóng 3
\(y=35i_2=42mm\)
\(\rightarrow chọn.B\)

Chọn đáp án C
Ta có 15 λ 1 = 12 λ 2 = 10 λ 3
Khoảng vân trung của 3 bức xạ là i T = λ D a = 15 λ 1 . D a = 15.0 , 4.10 − 6 .1 2.10 − 3 = 3.10 − 3 m
→ khoảng cách từ vân trắng thứ ba đến vân trắng trung tâm là x = 3 i T = 9 m m .

+ Khi vân sang của bức xạ λ 1 trùng với vân tối của bức xạ λ 2
k 1 k 2 + 0 , 5 = λ 2 λ 1 = 2 2 , 5 = 6 7 , 5 = ...
i 2 = λ 2 D a = 0 , 75 m m
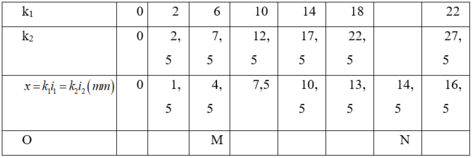
+ Trên đoạn MN có 4 vị trí vân sáng của bức xạ λ 1 trùng với vân tối của bức xạ λ 2

Đáp án D
Phương pháp: Coi sự giao thoa trùng vân giống như giao thoa ánh sáng đơn sắc, ta đi tìm khoảng vân trùng nhau.
Cách giải:
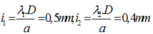
Vị trí vân sáng và vân tối thỏa mãn điều kiện :
![]()
Vì vân sáng trùng với vị trí vân tối nên ta có:
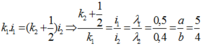
Coi đây là hiện tượng giao thoa với khoảng vân trùng nhau là:
![]()
Số vân trùng nhau trong khoảng MN thỏa mãn điều kiện :
![]()
![]()
![]()
Vậy có 15 giá trị k thỏa mãn






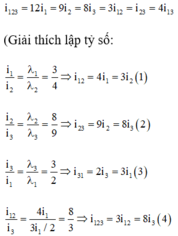




Vân tối bậc 13 của λ 3 trùng thì vân sang bậc 27 của λ 3 sẽ là vân trùng đầu tiên và do vân tối trùng nhau nên bậc của vân sang phải là số lẻ
Đáp án B