Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) An: "\(\forall x \in \mathbb R ,{x^2} \ge 0\)"
b) Bình: "\(\exists x \in ,{x^2} < 0\)"

a) “\(\forall x \in \mathbb{R},x + ( - x) = 0\)”
b) “\(\exists n \in \mathbb{N},{x^2} = 9\)”

P: "\(\forall n \in \mathbb N,\;{n^2} \ge n".\)
Q: "\(\exists \;a \in \mathbb R,\;a + a = 0".\)

a) \(\forall x\in\mathbb{R}:x+\left(-x\right)=0\) (đúng)
Phủ định là \(\exists x\in\mathbb{R}:x+\left(-x\right)\ne0\) (sai)
b) \(\forall x\in\mathbb{R}\)\ \(\left\{0\right\}:x.\dfrac{1}{x}=1\) (đúng
Phủ định là \(\exists x\in\mathbb{R}\)\ \(\left\{0\right\}:x.\dfrac{1}{x}\ne1\) (sai)
c) \(\exists x\in R:x=-x\) (đúng)
Phủ định là \(\forall x\in\mathbb{R}:x\ne-x\) (sai)

a) \(\exists a\in\mathbb{Z}:a=a^2\)
b) \(\forall x\in\mathbb{R}:x+0=x\)
c) \(\exists x\in\mathbb{Q}:x< \dfrac{1}{x}\)
d) \(\forall n\in\mathbb{N}:n>0\)

a) Phát biểu “Tích hai số thực trái dấu là một số thực âm” là một mệnh đề toán học.
b) Phát biểu “Mọi số tự nhiên đều là dương” là một mệnh đề toán học.
c) Phát biểu “Có sự sống ngoài Trái Đất” không là một mệnh đề toán học (vì không liên quan đến sự kiện Toán học nào).
d) Phát biểu “Ngày 1 tháng 5 là ngày Quốc tế Lao động” không là một mệnh đề toán học (vì không liên quan đến sự kiện Toán học nào).

a) \(\exists x \in \mathbb{Z},\;x \not{\vdots} \;x.\)
b) \(\forall x \in \mathbb{R},\;x + 0 = x.\)

Mệnh đề P đúng, bình phương của một số thực luôn lớn hơn hoặc bằng 0 (không âm).
Mệnh đề Q sai vì \({x^2} = 2 \Leftrightarrow x = \pm \sqrt 2 \notin \mathbb Q\), do đó không có số hữu tỉ nào mà bình phương của nó bằng 2.
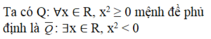
Trong tiết học môn Toán, Nam phát biểu: “Mọi số thực đều có bình phương khác 1”.
Mai phát biểu: “Có một số thực mà bình phương của nó bằng 1”
a) Phát biểu của Nam là sai. (chẳng hạn 1 và -1)
Phát biểu của Mai là đúng, số thực đó là 1 và -1.
b) Phát biểu của Nam: "\(\forall x \in \mathbb{R},\;{x^2} \ne 1\)".
Phát biểu của Mai: "\(\exists \;x \in \mathbb{R},{x^2} = 1\)".