Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án : D
Ta xét hai trường hợp sau:
+) TH1.
chọn d có 3 cách,b có 4 cách, c có 3 cách nên có 3.4.3 = 36 số thỏa mãn.
+) TH2. 
Với d = 0 thì chọn a có 4 cách, c có 3 cách nên có 4.3 = 12 số thỏa mãn.
Với d khác 0, chọn d có 2 cách, a có 3 cách, c có 3 cách nên có 2.3.3 = 18 số thỏa mãn.
Tóm lại có tất cả 36 + 12 + 18 = 66 số thỏa mãn.
Ta có 
nên d ∈ {2;4;6;8}
·Với d=4; c=5, chọn a có 7 cách, chọn b có 6 cách nên có 7.6= 42 số thỏa mãn.
· Với d=2
1. Số cần lập có dạng 
chọn c có 6 cách nên có 6 số thỏa mãn.
2. Số cần lập có dạng 
chọn c có 6 cách nên có 6 số thỏa mãn
3. Số cần lập có dạng 
chọn a có 6 cách nên có 6 số thỏa mãn.
4. Số cần lập có dạng 
chọn a có 6 cách nên có 6 số thỏa mãn.
Như vậy với d=2 có 6+6+6+6=24 số thỏa mãn.
· Tương tự với d=6; d=8
Vậy có tất cả 42+3.24=114 số thỏa mãn.
Chọn B.
Chọn B.
? TH1: 1 nằm ở vị trí đầu
4 chữ số phía sau có: 7.6.5.4 =840 (cách)
? TH2: 1 không nằm ở đầu
Có 2 cách chọn vị trí cho số 1
Vị trí đầu có 6 cách
3 vị trí còn lại có 6.5.4 = 120 (cách)
Số các số thỏa là: 2.6.120 = 1440
Số cách chọn là: 840 + 1440 = 2280 (cách)
Đáp án D
Phương pháp: Xét từng trường hợp: chữ số đầu tiên bằng 1, chữ số thứ hai bằng 1, chữ số thứ ba bằng 1.
Cách giải: Gọi số đó là a b c d e
- TH1: a = 1
+ b có 7 cách chọn.
+ c có 6 cách chọn.
+ d có 5 cách chọn.
+ e có 4 cách chọn.
Nên có: 7.6.5.4 = 840 số
- TH2: b = 1
+ a ≠ b , a ≠ 0 , nên có 6 cách chọn.
+ c có 6 cách chọn.
+ d có 5 cách chọn.
+ e có 4 cách chọn.
Nên có: 6.6.5.4 = 720 số.
- TH3: c = 1.
+ a ≠ c , a ≠ 0 , nên có 6 cách chọn.
+ b có 6 cách chọn.
+ d có 5 cách chọn.
+ e có 4 cách chọn.
Nên có 6.6.5.4 = 720 số.
Vậy có tất cả 840 + 720 + 720 = 2280 số.
gọi số cần tìm là abcdef( có gạch trên đầu b nhé)
với đk a#0 abcdef khác nhau
1; a có 8 cách chọn
b có 7 cách chọn
c có 6 cách chọn
d có 5 cách chọn
e có có 4 cách chọn
f có 3 cách chọn
=> có 20160 số tmycbt
Số tự nhiên có 6 chữ số có dạng: \(\overline{abcdef}\)
TH1: \(a=3\)
f có 2 cách chọn.
\(\overline{bcde}\) có \(A^4_6\) cách lập.
\(\Rightarrow\) Lập được \(2A^4_6=720\) số tự nhiên thỏa mãn.
TH2: \(b=3\)
Nếu \(f=0\Rightarrow\) a có 6 cách chọn.
\(\overline{cde}\) có \(A_5^3\) cách lập.
\(\Rightarrow\) Lập được \(6.A_5^3=360\) số tự nhiên thỏa mãn.
Nếu \(f=5\Rightarrow\) a có 5 cách chọn.
\(\overline{cde}\) có \(A_5^3\) cách lập.
\(\Rightarrow\) Lập được \(5A_5^3=300\) số tự nhiên thỏa mãn.
Vậy lập được \(720+360+300=1380\) số tự nhiên thỏa mãn.
Ta có 
.
Với d=4 thì c=5 , chọn a có 7 cách, chọn b có 7 cách nên có 7.7 = 49 số thỏa mãn.
Với d=2:
+) Dạng 
chọn c có 6 cách nên có 6 số thỏa mãn.
+) Dạng 
chọn a có 6 cách nên có 6 số thỏa mãn.
Đổi chỗ 4 và 5 thì có số thỏa mãn.
Tương tự với d=6; d=8 nên có tất cả 42 + 3.24 = 114 số thỏa mãn
Chọn B.
Ta xét hai trường hợp sau:
+) TH1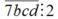
, chọn d có 3 cách, b có 4 cách, c có 3 cách nên có
3.4.3 = 36 số thỏa mãn.
+) TH2.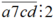
Với d = 0 thì có 4 cách chọn a, c có 3 cách nên có 4.3 = 12 số thỏa mãn.
Với d ≠ 0, chọn d có 2 cách, a có 3 cách, c có 3 cách nên có 2.3.3 = 18 số thỏa mãn.
Tóm lại có tất cả 36 + 12 + 18 = 66 số thỏa mãn.
Chọn D,