Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

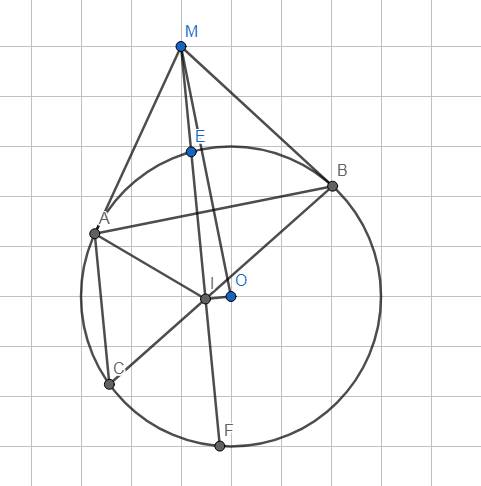
*Mấu chốt bài này là c/m 5 điểm M,A,I,O,B nằm trên cùng 1 đg tròn.
- Ta có: △OAM vuông tại A, △OBM vuông tại B.
\(\Rightarrow\)△OAM, △OBM nội tiếp đường tròn đường kính OM.
\(\Rightarrow\)AMBO nội tiếp đường tròn đường kính OM (1).
- Ta có AC//EF \(\Rightarrow\widehat{ACB}=\widehat{MIB}\) (2 góc so le trong).
- Trong (O) có:
\(\widehat{ACB}\) là góc nội tiếp chắn cung AB.
\(\widehat{MAB}\) là góc tạo bởi tia tiếp tuyến MA và dây cung AB.
\(\Rightarrow\widehat{ACB}=\widehat{MAB}\)
\(\Rightarrow\widehat{MAB}=\widehat{MIB}\). Do đó AIBM nội tiếp (2). (2 góc cùng nhìn 1 cạnh bằng nhau).
\(\left(1\right),\left(2\right)\Rightarrow\)A,M,B,O,I cùng nằm trên đường tròn đường kính OM.
\(\Rightarrow\)△OIM nội tiếp đường tròn đường kính OM.
\(\Rightarrow\)△OIM vuông tại I nên OI vuông góc với EF tại I.
Trong (O): EF là dây cung, OI là 1 phần đường kính, \(OI\perp EF\) tại I..
\(\Rightarrow\)I là trung điểm EF (đpcm).

a: góc MAO+góc MBO=180 độ
=>MAOB nội tiếp
b: Xét ΔMAC và ΔMDA có
góc MAC=góc MDA
góc AMC chung
=>ΔMAC đồng dạng với ΔMDA
=>MA/MD=MC/MA
=>MA^2=MD*MC
Vì \(\angle MAE\) là góc tạo bởi tiếp tuyến MA và dây cung AE nên bằng góc nội tiếp chắn cung AE \(\Rightarrow=\angle MKA\)
Xét \(\Delta MAE\) và \(\Delta MKA:\) Ta có: \(\left\{{}\begin{matrix}\angle KMAchung\\\angle MAE=\angle MKA\end{matrix}\right.\)
\(\Rightarrow\Delta MAE\sim\Delta MKA\left(g-g\right)\Rightarrow\angle MEA=\angle MAK\)