Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

EP // MF (EP là đường trung bình trong ∆BAF) và EP = AF / 2 = MF => MENF là hình bình hành.
=> MP và EF cắt nhau tại trung điểm I.
FN // DE và FN = DE / 2 = QE => FQEN là hình bình hành => QN và EF cắt nhau tại trung điểm I
=> MP và QN cắt nhau tại trung điểm của chúng => MNPQ là hình bình hành

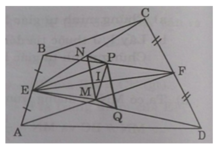
a) Xét tam giác ABF có:
E là trung điểm của AB
P là trung điểm của BF
⇒ EP là đường trung bình của ΔABF
⇒ EP // AF và EP = AF/2
M là trung điểm AF (gt)
⇒ MF = AF/2
Do đó EP // MF và EP = MF. Vậy EPFM là hình bình hành
I là giao điểm của hai đường chéo MP và EF nên I là trung điểm của MP.
b) Do tứ giác EPFM là hình bình hành nên I là trung điểm của EF.
Chứng minh tương tự ta có ENFQ là hình bình hành mà I là trung điểm của EF ⇒ I là trung điểm của NQ (2)
Từ (1) và (2) ⇒ MNPQ là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).

Bài 1.
EP // MF (EP là đường trung bình trong ∆BAF) và EP = AF / 2 = MF => MENF là hình bình hành.
=> MP và EF cắt nhau tại trung điểm I.
FN // DE và FN = DE / 2 = QE => FQEN là hình bình hành => QN và EF cắt nhau tại trung điểm I
=> MP và QN cắt nhau tại trung điểm của chúng => MNPQ là hình bình hành

a) Xét \(\Delta ABF\) có:
E là trung điểm của AB
P là trung điểm của BF
\(\Rightarrow EP\) là trug điểm của \(\Delta ABF\)
=> EP//AF và \(EP=\frac{AF}{2}\)
M là trung điểm AF (gt)
\(\Rightarrow MF=\frac{AF}{2}\)
=> I là giao điểm của hai đường chéo MP và EF nên I là trung điểm của MP.
b) Do tứ giác EPFM là hình bình hành nên I là trung điểm của EF.
Chứng minh tương tự ta có ENFQ là hình bình hành mà I là trung điểm của EF
=> I là trung điểm của NQ (1)
=> MNPQ là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).