Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Không gian mẫu gồm 20 phần tử được mô tả như sau:
Ω = {(1; 2), (2; 1), (1; 3), (3; 1), (1; 4), (4; 1), (1; 5), (5; 1), (2; 3), (3; 2), (2; 4), (4; 2), (2; 5), (5; 2), (3; 4), (4; 3), (3; 5), (5; 3), (4; 5), (5; 4)}
b. Xác định các biến cố sau:
+ A: "Chữ số sau lớn hơn chữ số trước"
A = {(1; 2), (1; 3), (1; 4), (1; 5), (2; 3), (2; 4), (2; 5), (3; 4), (3; 5), 4; 5)}
+ B: "Chữ số trước gấp đôi chữ số sau"
B = {(2; 1), (4; 2)}
+ C: "Hai chữ số bằng nhau".
C = ∅

Phép thử T được xét là: "Từ hộp đã cho, lấy ngẫu nhiên liên tiếp hai lần mỗi lần một quả và xếp theo thứ tự từ trái qua phải".
a) Mỗi một kết quả có thể có của phép thử T là một chỉnh hợp chập 2 của 5 quả cầu đã được đánh số 1, 2, 3, 4, 5. Do đó số các kết quả có thể có của phép thử T là
A25 = 20, và không gian mẫu của phép thử T bao gồm các phần tử sau:
Ω = {(1, 2), (2, 1), (1, 3), (3, 1), (1, 4), (4, 1), (1, 5), (5, 1), (2, 3), (3, 2), (2, 4), (4, 2), (2, 5), (5, 2), (3, 4), (4, 3), (3, 5), (5, 3), (4, 5), (5, 4)},
trong đó (i, j) là kết quả: "Lần đầu lấy được quả cầu đánh số j (xếp bên phải)",
1 ≤ i, j ≤ 5.
b) A = {(1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5)};
B = {(2, 1), (4, 2)};
C = Φ.

Chọn D
Chọn ngẫu nhiên một quả trong 30 quả có 30 cách. Vậy n ( Ω ) = 30.
Gọi A là biến cố: “lấy được quả cầu màu xanh”.
Ta có n(A) = 20 => P(A) = 2 3
Gọi B là biến cố: “lấy được quả cầu ghi số lẻ”.
Ta có n(B) = 15 => P(B) = 1 2 .
Số quả cầu vừa màu xanh vừa ghi số lẻ: 10 (quả).
Xác suất để lấy được quả cầu vừa màu xanh vừa ghi số lẻ: 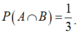
Xác suất để lấy được quả cầu màu xanh hay ghi số lẻ:
![]()
![]()

Không gian mẫu: \(C_{15}^3=455\)
Số cách chọn 3 quả sao cho vừa khác màu vừa khác số:
\(4.4.4=64\)
Xác suất: \(P=\dfrac{64}{455}\)

- Số cách lấy ngẫu nhiên 2 quả cầu: \(n\left( \Omega \right) = C_9^2 = 36\)
- Số cách lấy 2 quả khác màu là:
+ 1 quả màu xanh và 1 quả màu vàng: \(C_4^1 \times C_3^1 = 12\)
+ 1 quả màu xanh và 1 quả màu đỏ: \(C_4^1 \times C_2^1 = 8\)
+ 1 quả màu đỏ và 1 quả màu vàng: \(C_2^1 \times C_3^1 = 6\)
=> Tổng số cách lấy ra 2 quả khác màu là: 26 cách
- Số cách lấy 2 quả khác màu trùng số:
+ 2 quả cùng là số 1: \(C_3^2 = 3\)
+ 2 quả cùng là số 2: \(C_3^2 = 3\)
+ 2 quả cùng là số 3: \(C_2^2 = 1\)
=> Tổng số cách lấy ra 2 quả khác màu trùng số là: 7 cách
=> Số cách lấy ra 2 quả khác màu khác số là: 26 – 7 = 19 (cách)
=> Xác suất để lấy ra 2 quả khác màu khác số là: \(P = \frac{{19}}{{36}}\)

Xác suất lấy ra quả cầu không có số 1 hoặc số 5 từ túi đầu tiên: \(\frac{8}{{10}} = \frac{4}{5}\)
Xác suất lấy được quả cầu không có số 1 hoặc số 5 từ túi thứ hai là: \(\frac{8}{{10}} = \frac{4}{5}\)
Vì lấy ngẫu nhiên từ hai túi khác nhau một quả cầu nên hai biến cố quả cầu lấy ra mỗi túi không có số 1 hoặc số 5 là độc lập.
Vậy xác suất để trong hai quả cầu được lấy ra không có quả cầu nào ghi số 1 hoặc ghi số 5 là: \(\frac{4}{5}.\frac{4}{5} = \frac{{16}}{{25}}\)

Đáp án A
Gọi ![]() là không gian mẫu.
là không gian mẫu.
Ta có ![]()
Gọi D là biến cố: lấy được 2 quả cầu không trắng.
Ta có
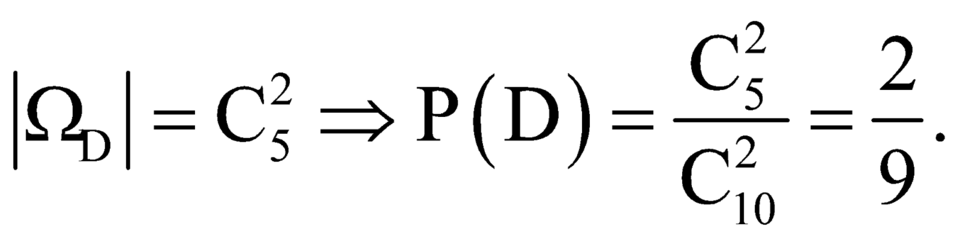
\(n\left(\Omega\right)=25\)
A: là số trước nhỏ hơn số sau
TH1 quả đầu bóc dính số 1 : 4 cách
TH2 quả đầu bóc dính số 2 : 3 cách
TH3 quả đầu bóc dính số 3 : 2 cách
TH4 quả đầu bóc dính số 4 : 1 cách
\(\Leftrightarrow n\left(A\right)=4+3+2+1=10\)
\(\Rightarrow P\left(A\right)=\dfrac{2}{3}\)