
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì cái này có hai chiều lên ta phải CM hai lần
(+) nếu 2 (u^2 - v^2) = 3uv => u = 2v
TA có 2( u^2 - v^2) = 3uv => 2u^2 - 2v^2 - 3uv = 0 => 2u^2 - 4uv + uv - 2v^2 = 0
=> 2u(u - 2v) + v ( u - 2v) = 0
=> ( 2u + v )( u - 2v) = 0
=> 2u + v = 0 hoặc u - 2v = 0 => u = 2v
(+) CM ngược lại

a,\(=\left(\frac{3}{5}x+\frac{2}{7}y\right)^2=\left(\frac{3}{5}.5+\frac{2}{7}.\left(-7\right)\right)^2=0\)
\(b,=\left(\frac{5}{4}u^2v+\frac{2}{25}v^2\right)^2=\left(\frac{5}{4}.\left(\frac{2}{5}\right)^2.5+\frac{2}{25}.5^2\right)^2=3^2=9\)

1. \(3x\left(x^2+2y\right)^2-12xy\left(x^2+y\right)\)\(=3x\left(x^4+4x^2y+4y^2\right)-12x^3y-12xy^2\)
\(=3x^5+12x^3y+12xy^2-12x^3y-12xy^2=3x^5\)
2. \(u^2v^2\left(u+v\right)^2-\left(u^2v+uv^2\right)^2\)
\(=u^2v^2\left(u^2+2uv+v^2\right)-\left(u^4v^2+2u^3v^3+u^2v^4\right)\)
\(=u^4v^2+2u^3v^3+u^2v^4-u^4v^2-2u^3v^3-u^2v^4=0\)

a) ∀ x , y ∈ ℝ
b) Chú ý: A 2 + B 2 ≥ 0 với ∀ A , B . Dấu "=" xảy ra khi A = 0 B = 0
Từ đó tìm được điều kiện xác định là: u ≠ 1 và v ≠ -2.

Bài 1:
a) Ta có: \(VT=\frac{-u^2+3u-2}{\left(u+2\right)\left(u-1\right)}\)
\(=\frac{-\left(u^2-3u+2\right)}{\left(u+2\right)\left(u-1\right)}\)
\(=\frac{-\left(n^2-u-2u+2\right)}{\left(u+2\right)\left(u-1\right)}\)
\(=\frac{-\left[u\left(u-1\right)-2\left(u-1\right)\right]}{\left(u+2\right)\left(u-1\right)}\)
\(=\frac{-\left(u-1\right)\left(u-2\right)}{\left(u+2\right)\left(u-1\right)}\)
\(=\frac{2-u}{u+2}\)(1)
Ta có: \(VP=\frac{u^2-4u+4}{4-u^2}\)
\(=\frac{\left(u-2\right)^2}{-\left(u-2\right)\left(u+2\right)}\)
\(=\frac{-\left(u-2\right)}{u+2}\)
\(=\frac{2-u}{u+2}\)(2)
Từ (1) và (2) suy ra \(\frac{-u^2+3u-2}{\left(u+2\right)\left(u-1\right)}=\frac{u^2-4u+4}{4-u^2}\)
b) Ta có: \(VT=\frac{v^3+27}{v^2-3v+9}\)
\(=\frac{\left(v+3\right)\left(v^3-3u+9\right)}{v^2-3u+9}\)
\(=v+3=VP\)(đpcm)
Bài 2:
a) Ta có: \(\frac{3x^2-2x-5}{M}=\frac{3x-5}{2x-3}\)
\(\Leftrightarrow\frac{3x^2-5x+3x-5}{M}=\frac{3x-5}{2x-3}\)
\(\Leftrightarrow\frac{x\left(3x-5\right)+\left(3x-5\right)}{M}=\frac{3x-5}{2x-3}\)
\(\Leftrightarrow\frac{\left(3x-5\right)\left(x+1\right)}{M}=\frac{3x-5}{2x-3}\)
\(\Leftrightarrow M=\frac{\left(3x-5\right)\left(x+1\right)\left(2x-3\right)}{3x-5}\)
\(\Leftrightarrow M=\left(x+1\right)\left(2x-3\right)\)
\(\Leftrightarrow M=2x^2-3x+2x-3\)
hay \(M=2x^2-x-3\)
Vậy: \(M=2x^2-x-3\)
b) Ta có: \(\frac{2x^2+3x-2}{x^2-4}=\frac{M}{x^2-4x+4}\)
\(\Leftrightarrow\frac{2x^2+4x-x-2}{\left(x-2\right)\left(x+2\right)}=\frac{M}{\left(x-2\right)^2}\)
\(\Leftrightarrow\frac{2x\left(x+2\right)-\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\frac{M}{\left(x-2\right)^2}\)
\(\Leftrightarrow\frac{\left(x+2\right)\left(2x-1\right)}{\left(x+2\right)\left(x-2\right)}=\frac{M}{\left(x-2\right)^2}\)
\(\Leftrightarrow\frac{M}{\left(x-2\right)^2}=\frac{2x-1}{x-2}\)
\(\Leftrightarrow M=\frac{\left(2x-1\right)\left(x-2\right)^2}{\left(x-2\right)}\)
\(\Leftrightarrow M=\left(2x-1\right)\left(x-2\right)\)
\(\Leftrightarrow M=2x^2-4x-x+2\)
hay \(M=2x^2-5x+2\)
Vậy: \(M=2x^2-5x+2\)
Bài 3:
a) Ta có: \(\frac{x+1}{N}=\frac{x^2-2x+4}{x^3+8}\)
\(\Leftrightarrow\frac{x+1}{N}=\frac{x^2-2x+4}{\left(x+2\right)\left(x^2-2x+4\right)}\)
\(\Leftrightarrow\frac{x+1}{N}=\frac{1}{x+2}\)
\(\Leftrightarrow N=\left(x+1\right)\left(x+2\right)\)
hay \(N=x^2+3x+2\)
Vậy: \(N=x^2+3x+2\)
n) Ta có: \(\frac{\left(x-3\right)\cdot N}{3+x}=\frac{2x^3-8x^2-6x+36}{2+x}\)
\(\Leftrightarrow\frac{N\cdot\left(x-3\right)}{x+3}=\frac{2x^3+4x^2-12x^2-24x+18x+36}{x+2}\)
\(\Leftrightarrow\frac{N\cdot\left(x-3\right)}{\left(x+3\right)}=\frac{2x^2\left(x+2\right)-12x\left(x+2\right)+18\left(x+2\right)}{x+2}\)
\(\Leftrightarrow\frac{N\cdot\left(x-3\right)}{x+3}=\frac{\left(x+2\right)\left(2x^2-12x+18\right)}{x+2}\)
\(\Leftrightarrow\frac{N\cdot\left(x-3\right)}{x+3}=2x^2-12x+18\)
\(\Leftrightarrow\frac{N\cdot\left(x-3\right)}{x+3}=2x^2-6x-6x+18=2x\left(x-3\right)-6\left(x-3\right)=2\cdot\left(x-3\right)^2\)
\(\Leftrightarrow N\cdot\left(x-3\right)=\frac{2\left(x-3\right)^2}{x+3}\)
\(\Leftrightarrow N=\frac{2\left(x-3\right)^2}{x+3}:\left(x-3\right)=\frac{2\left(x-3\right)^2}{\left(x+3\right)\left(x-3\right)}\)
\(\Leftrightarrow N=\frac{2\left(x-3\right)}{x+3}\)
hay \(N=\frac{2x-6}{x+3}\)
Vậy: \(N=\frac{2x-6}{x+3}\)

u^2v^2(u+v)^2-(u^2v+uv^2)^2 - Step-by-Step Calculator - Symbolab
Tham khảo ở đó nhé!

a, \(x^2+2x\left(y+1\right)+y^2+2y+1=\left(x^2+2xy+y^2\right)+\left(2x+2y\right)+1\)
\(=\left(x+y\right)^2+2\left(x+y\right)+1=\left(x+y+1\right)^2\)
b, \(u^2+v^2+2u+2v+2\left(u+1\right)\left(v+1\right)+2\)
\(=u^2+v^2+2u+2v+2uv+2u+2v+2+2\)
\(=\left(u^2+2uv+v^2\right)+\left(4u+4v\right)+4\)
\(=\left(u+v\right)^2+4\left(u+v\right)+2^2=\left(u+v+2\right)^2\)
1.
a) \(A=x^2+2x\left(y+1\right)+y^2+2y+1\)
\(A=x^2+2x\left(y+1\right)+\left(y+1\right)^2\)
\(A=\left(x+y+1\right)^2\)
b) \(B=u^2+v^2+2u+2v+2\left(u+1\right)\left(v+1\right)+2\)\(B=u^2+v^2+2u+2v+2\left(u+1\right)\left(v+1\right)+1+1\)\(B=\left(u^2+2u+1\right)+2\left(u+1\right)\left(v+1\right)+\left(v^2+2v+1\right)\)\(B=\left(u+1\right)^2+2\left(u+1\right)\left(v+1\right)+\left(v+1\right)^2\)\(B=\left(u+1+v+1\right)^2=\left(u+v+2\right)^2\)
tik mik nha !!!
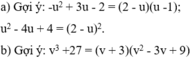
chẳng hỉu gì cả@@@@@@@@@@@@@@@@@@
phân tích tử trc cho đỡ mất công gõ cả ps
u4-u3v+u2v2-uv3
=(u4+u2v2)-(u3v+uv3)
=u2(u2+v2)-uv(u2+v2)
=(u2-uv)(u2+v2)
=u(u-v)(u2+v2)
Thay vào ta có \(\frac{u\left(u-v\right)\left(u^2+v^2\right)}{u^2+v^2}=u\left(u-v\right)=u^2-uv\)