Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trên hình vẽ, xét hai cặp tam giác đồng dạng:
ΔA’B’F’ và ΔOIF’; ΔOAB và ΔOA’B’.
Từ hệ thức đồng dạng ta có:
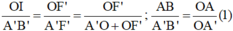
Vì AB = OI (tứ giác BIOA là hình chữ nhật)
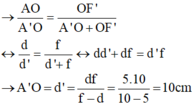
Từ (1) và (2) suy ra:
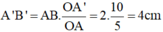
Vậy ảnh cách kính 10cm và cao 4cm.

Đáp án: A
Ảnh cao gấp 4 lần vật nên khoảng cách từ ảnh đến thấu kính gấp 4 lần khoảng cách từ vật đến thấu kính
=> d' = 40 cm
Vì ảnh là ảnh ảo.
Áp dụng công thức thấu kính hội tụ với ảnh ảo ta có:
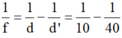
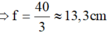

Khoảng cách từ ảnh đến thấu kính là:
Áp dụng công thức tính thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow d'=\dfrac{d.f}{d-f}=\dfrac{8.4}{8-4}=8\left(cm\right)\)
Chiều cao của ảnh:
Ta có: \(\dfrac{d}{d'}=\dfrac{h}{h'}\Rightarrow h'=\dfrac{d'.h}{d}=\dfrac{8.2}{8}=2\left(cm\right)\)

Đáp án B
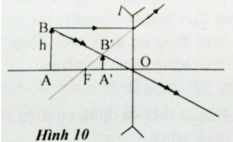
Từ tam giác đồng dạng
Ta có: AB/A'B' = d/d' (1)
Mặt khác:
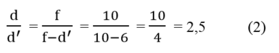
=> AB = A’B’ . 2,5 = 5 (cm)
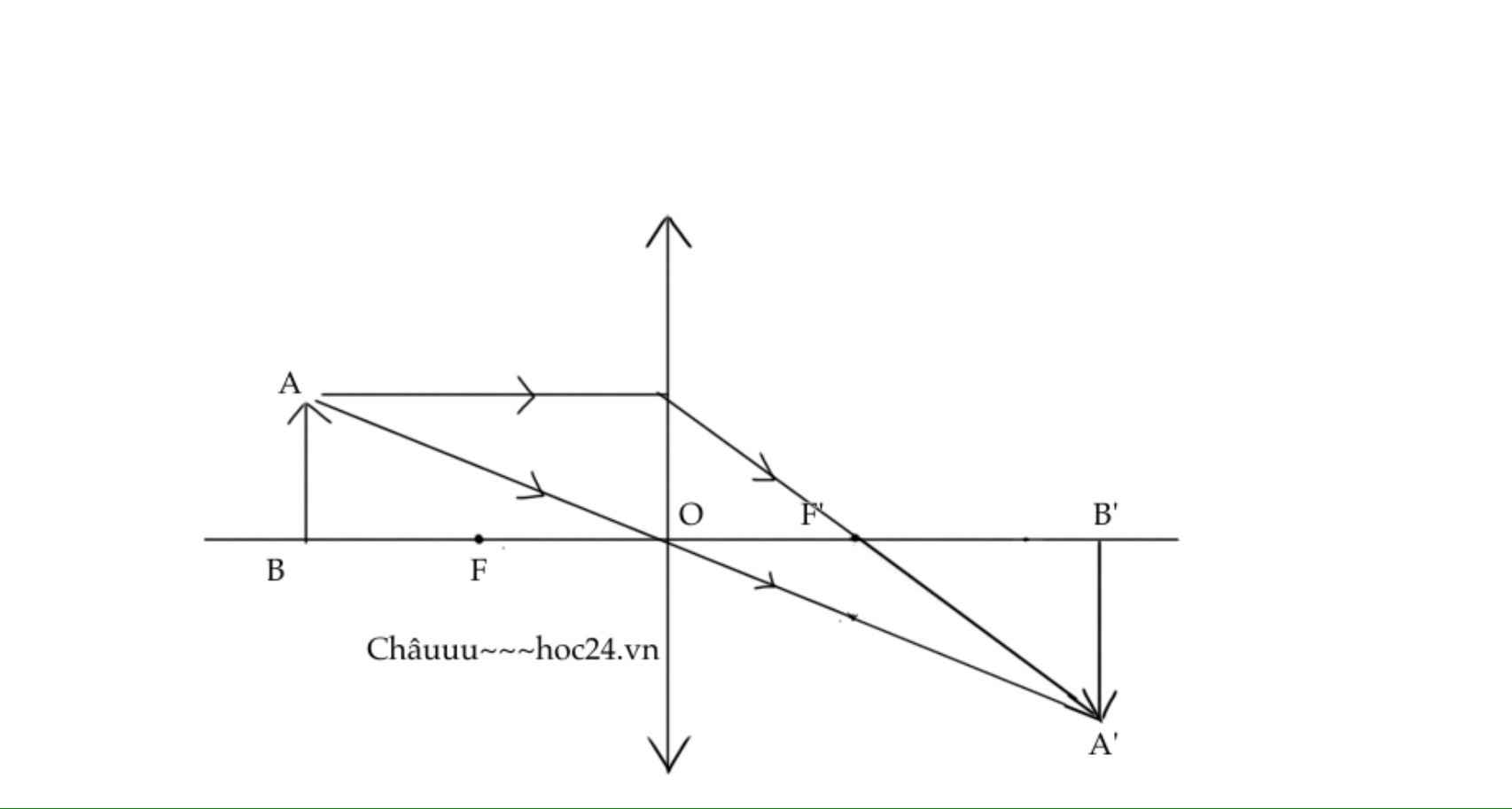
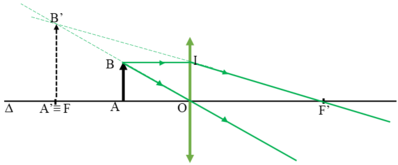
Ta có hình vẽ 2, xét tam giác đồng dạng OAB và OA’B’ ta được công thức:
Mặt khác d’ = 2d/4 = 2.10/4 = 5(cm)
Vậy f/(5-f ) = 2 ⇔ f = 10 – 2f => f = 10/3 (cm)