Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tam giác ABC nhọn:
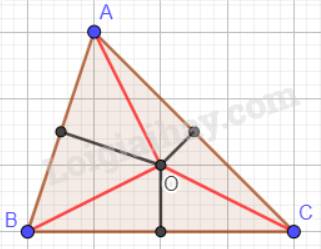
b) Tam giác ABC vuông tại A:
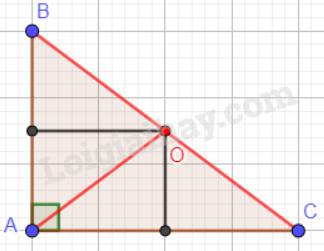
c) Tam giác ABC có góc A tù:
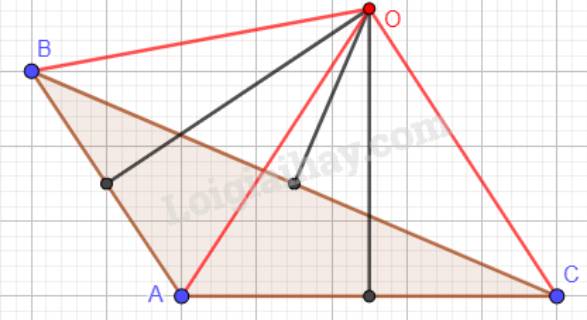

a)

Nhận xét: H là một điểm nằm trong tam giác ABC.
b)

Nhận xét: H trùng với đỉnh A của tam giác ABC.
c)
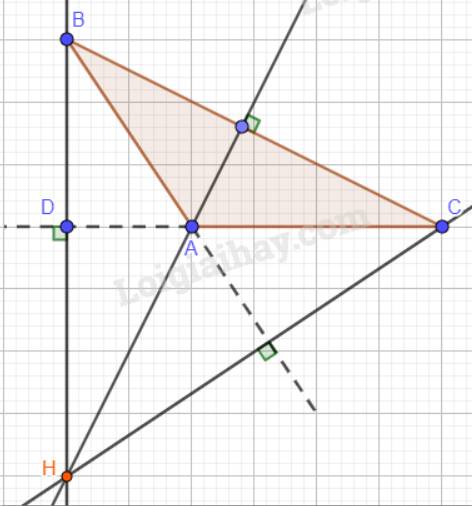
Nhận xét: H nằm ngoài tam giác ABC.

Tham khảo:
Theo giả thiết ta có :
OA = OB, MA = MB ( do M là trung điểm AB )
\( \Rightarrow \) MO là đường trung trực của đoạn thẳng AB
\( \Rightarrow \) MO vuông góc với AB
Theo giả thiết ta có :
OA = OC, PC = PA ( do P là trung điểm AC )
\( \Rightarrow \) PO là đường trung trực của đoạn thẳng AC
\( \Rightarrow \) PO vuông góc với AC
Theo giả thiết ta có :
OC = OB, NC = NB ( do N là trung điểm BC )
\( \Rightarrow \) NO là đường trung trực của đoạn thẳng BC
\( \Rightarrow \) NO vuông góc với BC

O cách đều 3 đỉnh của tam giác ABC
\( \Rightarrow \) \(OA = OB = OC\)
\( \Rightarrow \) \(\Delta OAB\) cân tại O.
Giả sử O là trung điểm BC
\( \Rightarrow \widehat {OAB} = \widehat {OBA}\)
\(\Delta OAC\) cân tại O
\( \Rightarrow \widehat {OAC} = \widehat {OCA}\)
Xét tam giác ABC có
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^0}\\ \Rightarrow \widehat A + \widehat {OAB} + \widehat {OAC} = {180^0}\\ \Rightarrow \widehat A + \widehat A = {180^0}\\ \Rightarrow \widehat A = {90^0}\end{array}\)
Vậy nếu O nằm trên một cạnh của tam giác ABC thì ABC là một tam giác vuông.

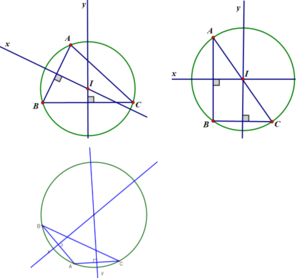
Đường tròn đi qua ba đỉnh của tam giác ABC gọi là đường tròn ngoại tiếp tam giác đó.
Để vẽ đường tròn ta cần:
+ Vẽ đường trung trực y của cạnh BC.
+ Vẽ dường trung trực x của cạnh AB.
+ x cắt y tại I là tâm của đường tròn cần vẽ.
+ Vẽ đường tròn tâm I bán kính IA.
Nhận xét:
- Tam giác nhọn có tâm đường tròn ngoại tiếp nằm trong tam giác.
- Tam giác vuông có tâm đường tròn ngoại tiếp là trung điểm của cạnh huyền (chứng minh bài 56).
- Tam giác tù có tâm đường tròn ngoại tiếp nằm ngoài tam giác.

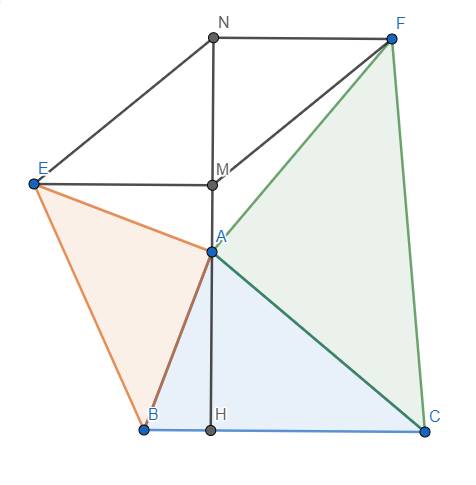
a) Do tam giác AEB vuông cân tại A nên \(\left\{{}\begin{matrix}\widehat{EAB}=90^o\\AE=AB\end{matrix}\right.\)
Ta thấy \(\widehat{MEA}=\widehat{BAH}\) vì chúng cùng phụ với \(\widehat{EAM}\)
Xét 2 tam giác HAB vuông tại H và MEA vuông tại M, ta có:
\(AE=AB\left(cmt\right),\widehat{MEA}=\widehat{BAH}\left(cmt\right)\)
\(\Rightarrow\Delta HAB=\Delta MEA\left(ch-gn\right)\) \(\Rightarrow AH=ME\) (1)
Tương tự, ta cũng có \(\Delta HAC=\Delta NFA\Rightarrow HC=AN\) (2)
Từ (1) và (2) suy ra \(EM+HC=AH+AN\) hay \(EM+HC=HN\) (đpcm)
b) Từ \(\Delta HAC=\Delta NFA\Rightarrow AH=NF\)
Từ đó suy ra \(ME=NF\left(=AH\right)\)
Xét tam giác MNE và NMF, ta có:
\(ME=NF\left(cmt\right),\widehat{EMN}=\widehat{FNM}\left(=90^o\right)\), MN là cạnh chung.
\(\Rightarrow\Delta MNE=\Delta NMF\left(c.g.c\right)\)
\(\Rightarrow\widehat{ENM}=\widehat{FMN}\) \(\Rightarrow\) EN//FM (2 góc so le trong bằng nhau)
Ta có đpcm.
Tham khảo:
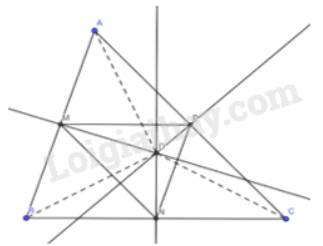
a) Vẽ 3 tam giác và xác định điểm O là giao điểm của 3 đường trung trực của 3 cạnh trong tam giác. Khi đó, O cách đều 3 đỉnh của tam giác
b) + Khi tam giác ABC nhọn, điểm O nằm trong tam giác.
+ Khi tam giác ABC vuông, điểm O nằm trên cạnh huyền.
+ Khi tam giác ABC tù, điểm O nằm ngoài tam giác.