Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(tự vẽ hình )
câu 4:
a) có AB2 + AC2 = 225
BC2 = 225
Pytago đảo => \(\Delta ABC\)vuông tại A
b) Xét \(\Delta MAB\)và \(\Delta MDC\)
MA = MD (gt)
BM = BC ( do M là trung điểm của BC )
\(\widehat{AMB}=\widehat{CMD}\)( hai góc đối đỉnh )
=> \(\Delta MAB\)= \(\Delta MDC\) (cgc)
c) vì \(\Delta MAB\)= \(\Delta MDC\)
=> \(\hept{\begin{cases}AB=DC\\\widehat{MAB}=\widehat{MDC}\end{cases}}\)
=> AB// DC
lại có AB \(\perp\)AC => DC \(\perp\)AC => \(\Delta KCD\)vuông tại C
Xét \(\Delta\) vuông ABK và \(\Delta\)vuông KCD:
AB =CD (cmt)
AK = KC ( do k là trung điểm của AC )
=> \(\Delta\)vuông AKB = \(\Delta\)vuông CKD (cc)
=> KB = KD
d. do KB = KD => \(\Delta KBD\)cân tại K
=> \(\widehat{KBD}=\widehat{KDB}\)(1)
có \(\Delta ADC\)vuông tại C => \(AD=\sqrt{AC^2+DC^2}=15\)
=> MD = 7.5
mà MB = 7.5
=> MB = MD
=> \(\Delta MBD\)cân tại M
=> \(\widehat{MBD}=\widehat{MDB}\)(2)
Từ (1) và (2) => \(\widehat{KBD}-\widehat{MBD}=\widehat{KDB}-\widehat{MDB}\)hay \(\widehat{KBM}=\widehat{KDM}\)
Xét \(\Delta KBI\)và \(\Delta KDN\)có:
\(\widehat{KBI}=\widehat{KDN}\)(cmt)
\(\widehat{KBD}\)chung
KD =KB (cmt)
=> \(\Delta KBI\)= \(\Delta KDN\)(gcg)
=> KN =KI
=. đpcm
câu 5:
a) Xét \(\Delta ABM\)và \(\Delta MDC\):
MA=MD(gt)
MB=MC (M là trung điểm của BC)
\(\widehat{BMA}=\widehat{DMC}\)( đối đỉnh )
=> \(\Delta BMA=\Delta CMD\)(cgc)
b) Xét \(\Delta\)vuông ABC
có AM là đường trung tuyến của tam giác
=> \(AM=\frac{1}{2}BC\)mà \(BM=MC=\frac{1}{2}BC\)(do M là trung điểm của BC )
=> AM = BM = MC
có MA =MD => AM = MD =MB =MC
=> BM +MC = AM +MD hay BC =AD
Xét \(\Delta BAC\)và \(\Delta DCA\)
AB =DC
AC chung
BC =DC
=> \(\Delta BAC\)= \(\Delta DCA\)(ccc)
c. Xét \(\Delta ABM\)
BM=AM
\(\widehat{ABM}\)= 600
=> đpcm

a) Xét tam giác ABM và tam giác ACM, ta có:
AB=AC(gt)
BM=CM(gt)
AM: cạnh chung
Do đó: tam giác ABM = tam giác ACM(c.c.c)
Vậy: Góc AMB = Góc AMC
Mà góc AMB + góc AMC = 180 độ =>
Góc AMB = Góc ACM = 180 độ / 2 = 90 độ
Vậy AM vuông góc với BC
b) Xét tam giác AMD và tam giác AME, ta có:
AD=AE (gt)
Góc DAM = Góc EAM ( theo câu a, cặp góc tương ứng )
AM: cạnh chung
Do đó: Tam giác AMD = tam giác AME (c.g.c)
c) Ta thấy: Góc EDM + Góc KDM = 180 độ ( kề bù )
Vậy ba điểm D,E,K thẳng hàng
=> tam giác ABC cân tại A
Xét ABM và ACM có:
AM chung
AB = AC
A1 = A2 (tam giác ABC cân tại A)
Vậy tam giác ABM = ACM
M1 = M2 ; M1 + M2 = 180 (2 góc kề bù)
=> M1 = M2 = 90
=> AM vuông góc BC

Lời giải:
a.
Do tam giác $ABC$ cân tại $A$ nên $AB=AC$
Xét tam giác $ABM$ và $ACM$ có:
$AB=AC$
$AM$ chung
$BM=CM$ (do $M$ là trung điểm $BC$)
$\Rightarrow \triangle ABM=\triangle ACM$ (c.c.c)
b.
Từ tam giác bằng nhau phần a suy ra $\widehat{BAM}=\widehat{CAM}$. Mà $AM$ nằm giữa $AB, AC$ nên $AM$ là tia phân giác $\widehat{BAC}$
Cũng từ tam giác bằng nhau phần a suy ra:
$\widehat{AMB}=\widehat{AMC}$
Mà $\widehat{AMB}+\widehat{AMC}=\widehat{BMC}=180^0$
$\Rightarrow \widehat{AMB}=180^0:2=90^0$
$\Rightarrow AM\perp BC$
c.
$AM\perp BC, M$ là trung điểm $BC$ nên $AM$ là đường trung trực của $BC$
$\Rightarrow$ mọi điểm $E\in AM$ đều cách đều 2 đầu mút B,C (theo tính chất đường trung trực)
$\Rightarrow EB=EC$
$\Rightarrow \triangle EBC$ cân tại $E$.

a/ Xét tg ABM và tg ACM có
AB = AC ( gt)
BM = CM ( gt)
AM chung
=> tg ABM = tg ACM (ccc)
b/ ( Trên tia đối của tia MA chứ ko phải AM nha )
Xét tg AMC và tg DMB, có
MC = MB (gt)
AM = MD ( gt)
^AMC = ^BMD ( đđ )
=> tg AMC = tg DMB ( cgc)
=> AC = BD
c/ tg ABC cân tại A có AM là đường trung tuyến
=> AM cũng là đường cao
=> AD vuông góc BC (1)
Lại có AM = MD , BM = MC ( gt) (2)
Từ (1), (2) => ABCD là hình thoi
=> AB // CD
d/ Theo đề : AI // BC , AI = BC
=> ABCI là hình bình hành
=> AB // CI
Mà AB // BC ( cmt )
=> I , C ,D thẳng hàng

a, Vì M là trung điểm cạnh BC => MB = MC
Xét △ABM và △ACM có:
AB = AC (gt)
MB = MC (cmt)
AM chung
=> △ABM = △ACM (c-c-c)
b, Vì △ABM = △ACM (cmt)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 góc tương ứng)
mà \(\widehat{AMB}+\widehat{AMC}=180^o\)
=> \(2\widehat{AMB}=180^o\)
=> \(\widehat{AMB}=90^o\)
=> AM ⊥ BC
c, Xét △ADM và △AEM có:
AD = AE(gt)
\(\widehat{A_1}=\widehat{A_2}\) (do ABM = ACM)
AM chung
=> △ADM = △AEM (c-g-c)

a: Xét ΔABM và ΔACM có
AB=AC
MB=MC
AM chung
Do đó: ΔABM=ΔACM
b: Ta có: ΔBAC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: Xét ΔAEH và ΔCEM có
EA=EC
góc AEH=góc CEM
EH=EM
Do đó: ΔAEH=ΔCEM
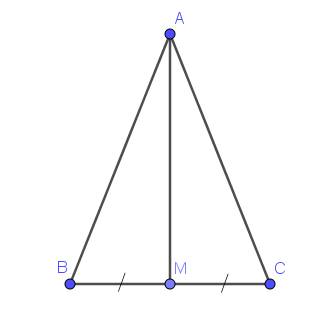
a) .....
b and c) ABC là tg cân tại A nên tg ABM=ACM và B đx C qua M= M là điểm thuộc trung trực tg ABC
Nb=Nc => AN là đg cao và trong tg cân thì dg cao = trung trực nên....
Hình bạn tự vẽ nha!
a) Xét 2 \(\Delta\) \(ABM\) và \(ACM\) có:
\(AB=AC\left(gt\right)\)
\(BM=CM\left(gt\right)\)
Cạnh AM chung
=> \(\Delta ABM=\Delta ACM\left(c-c-c\right).\)
b) Theo câu a) ta có \(\Delta ABM=\Delta ACM.\)
=> \(\widehat{BAM}=\widehat{CAM}\) (2 góc tương ứng).
=> \(AM\) là tia phân giác của \(\widehat{BAC}\) (1)
Xét 2 \(\Delta\) \(ABN\) và \(ACN\) có:
\(AB=AC\left(gt\right)\)
\(BN=CN\) (vì N là trung điểm của \(BC\))
Cạnh AN chung
=> \(\Delta ABN=\Delta ACN\left(c-c-c\right).\)
=> \(\widehat{BAN}=\widehat{CAN}\) (2 góc tương ứng).
=> \(AN\) là tia phân giác của \(\widehat{BAC}\) (2)
Từ (1) và (2) => \(AM,AN\) đều là tia phân giác của \(\widehat{BAC}.\)
=> \(A,M,N\) thẳng hàng.
c) Xét \(\Delta ABC\) có:
\(AB=AC\left(gt\right)\)
=> \(\Delta ABC\) cân tại A.
Có \(AN\) là đường phân giác (cmt).
=> \(AN\) đồng thời là đường trung trực của \(\Delta ABC.\)
=> \(AN\) là đường trung trực của \(BC.\)
Mà \(A,M,N\) thẳng hàng (cmt).
=> \(MN\) là đường trung trực của \(BC\left(đpcm\right).\)
Chúc bạn học tốt!