a) Để \(y = 8 \Leftrightarrow \frac{1}{2}{x^2} = 8 \Leftrightarrow {x^2} = 16 \Leftrightarrow x = 4\) hoăc \(x =  - 4\)

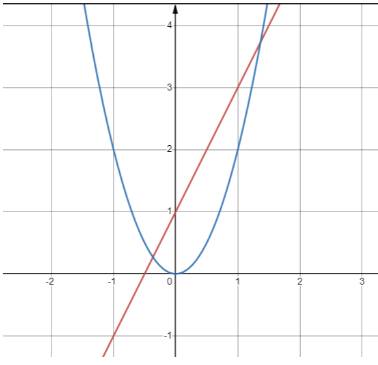
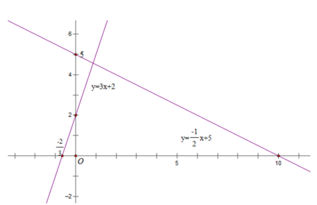
b) Vẽ đồ thị y=2x+1:

-Là đồ thị bậc nhất nên đồ thị là đường thẳng đi qua điểm có tọa độ (0; 1) và

(-1; -1)

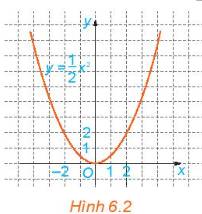
Vẽ đồ thị \(y = 2{x^2}\)

- Đi qua điểm (1; 2) ; (-1; 2);(0;0)

a, Bảng biến thiên:

Đồ thị hàm số:

b, Phương trình hoành độ giao điểm

\(-x^2+2x+3=4x-5\)

\(\Leftrightarrow x^2+2x-8=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-4\end{matrix}\right.\)

Nếu \(x=2\Rightarrow y=3\Rightarrow\left(2;3\right)\)

Nếu \(x=-4\Rightarrow y=-21\Rightarrow\left(-4;-21\right)\)

Tham khảo:

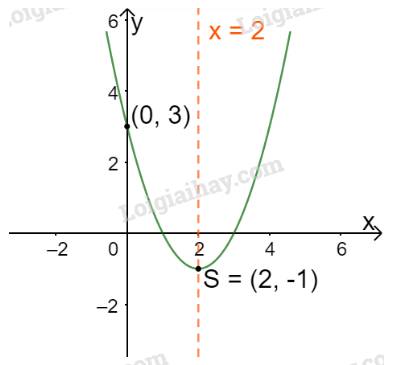
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = f(x) = {x^2} - 4x + 3\) là một parabol (P1):

+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.1}} = 2;{y_S} = {2^2} - 4.2 + 3 =  - 1.\)

+ Có trục đối xứng là đường thẳng \(x = 2\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);

+ Bề lõm quay lên trên vì \(a = 1 > 0\)

+ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).

Ta vẽ được đồ thị như hình dưới.

*So sánh với đồ thị hàm số ở Ví dụ 2a:

Giống nhau: Có chung trục đối xứng

Khác nhau:

Điểm đỉnh và giao điểm với trục tung của hai hàm số đối xứng với nhau qua trục Ox.

Bề lõm của (P) xuống dưới còn (P1) quay lên trên.

Nhận xét chung: Hai đồ thị này đối xứng với nhau qua trục Ox.

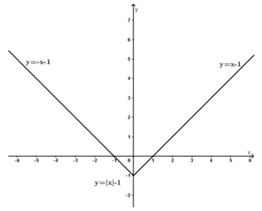
y = |x| - 1 hay

Vậy đồ thị hàm số y = |x| – 1 là hợp của hai nửa:

+ Nửa đồ thị là đường thẳng y = x – 1 trong khoảng (0; +∞).

+ Nửa đồ thị là đường thẳng y = –x – 1 trong khoảng (–∞; 0).

b: \(y=0\Leftrightarrow\left|2x-3\right|=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)

\(x=0\Leftrightarrow y=3\)

a: Tọa độ đỉnh là:

\(\left\{{}\begin{matrix}x=\dfrac{-\left(-3\right)}{2}=\dfrac{3}{2}\\y=-\dfrac{\left(-3\right)^2-4\cdot1\cdot4}{4\cdot1}=-\dfrac{9-16}{4}=\dfrac{7}{4}\end{matrix}\right.\)

Vì \(y=x^2-3x+4\) có a=1>0

nên hàm số sẽ đồng biến khi \(x>\dfrac{3}{2}\) và nghịch biến khi \(x< \dfrac{3}{2}\)

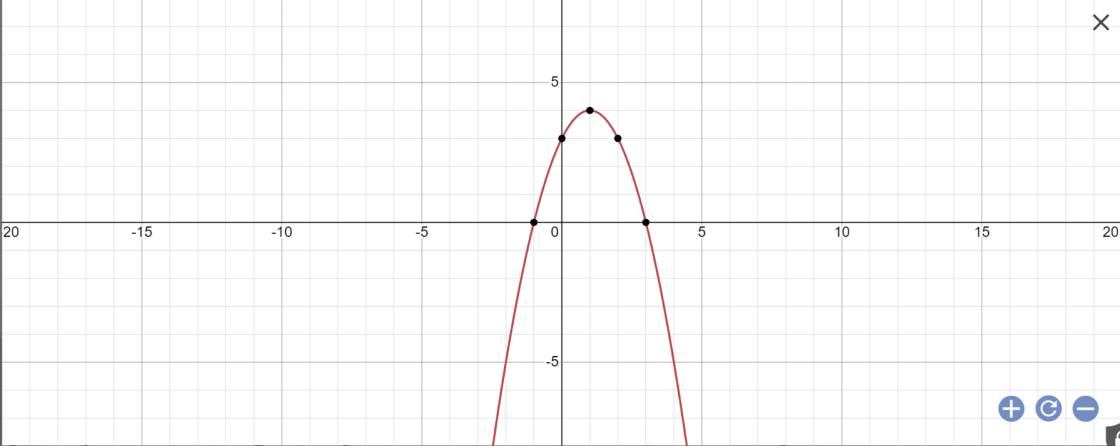
b: Tọa độ đỉnh là:

\(\left\{{}\begin{matrix}x=-\dfrac{2}{2\cdot\left(-1\right)}=\dfrac{-2}{-2}=1\\y=-\dfrac{2^2-4\cdot\left(-1\right)\cdot3}{4\cdot\left(-1\right)}=-\dfrac{4+12}{-4}=4\end{matrix}\right.\)

Vì \(y=-x^2+2x+3\) có a=-1<0

nên hàm số đồng biến khi x<1 và nghịch biến khi x>1