Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
2:
a: Thay m=0 vào (d), ta được:
\(y=\left(0+1\right)x-2=x-2\)
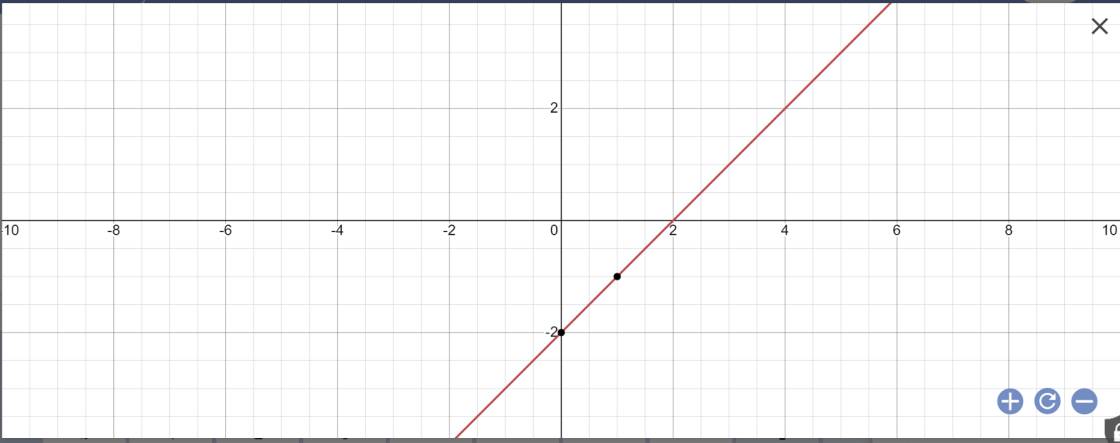
b: Thay x=1 vào y=x+1, ta được:
y=1+1=2
Thay x=1 và y=2 vào (d), ta được:
1(m+1)-2=2
=>m+1=4
=>m=3
c: Để \(\widehat{OAB}=45^0\) thì góc tạo bởi (d) với trục Ox bằng 45 độ
(d): y=(m+1)x-2
=>a=m+1
\(\Leftrightarrow tanOAB=a=m+1\)
=>m+1=tan45=1
=>m=0


\(a,B=\dfrac{2+3}{2.2+3}=\dfrac{5}{7}\\ b,A=\dfrac{\sqrt{x}+15-x-3\sqrt{x}+2x-\sqrt{x}-15}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ A=\dfrac{x-3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}}{\sqrt{x}+3}\\ c,P=AB=\dfrac{\sqrt{x}}{2\sqrt{x}-3}< \dfrac{1}{2}\Leftrightarrow\dfrac{\sqrt{x}}{2\sqrt{x}-3}-\dfrac{1}{2}< 0\\ \Leftrightarrow\dfrac{2\sqrt{x}-2\sqrt{x}+3}{2\left(2\sqrt{x}-3\right)}< 0\Leftrightarrow\dfrac{3}{2\left(2\sqrt{x}-3\right)}< 0\\ \Leftrightarrow2\sqrt{x}-3< 0\left(3>0\right)\\ \Leftrightarrow\sqrt{x}< \dfrac{3}{2}\Leftrightarrow0< x< \dfrac{9}{4}\)

b: B>0
=>\(\dfrac{1}{-x+\sqrt{x}}>0\)
=>\(-x+\sqrt{x}>0\)
=>\(x-\sqrt{x}< 0\)
=>\(\sqrt{x}\left(\sqrt{x}-1\right)< 0\)
=>\(\sqrt{x}-1< 0\)
=>\(\sqrt{x}< 1\)
=>0<=x<1
Kết hợp ĐKXĐ, ta được: 0<x<1

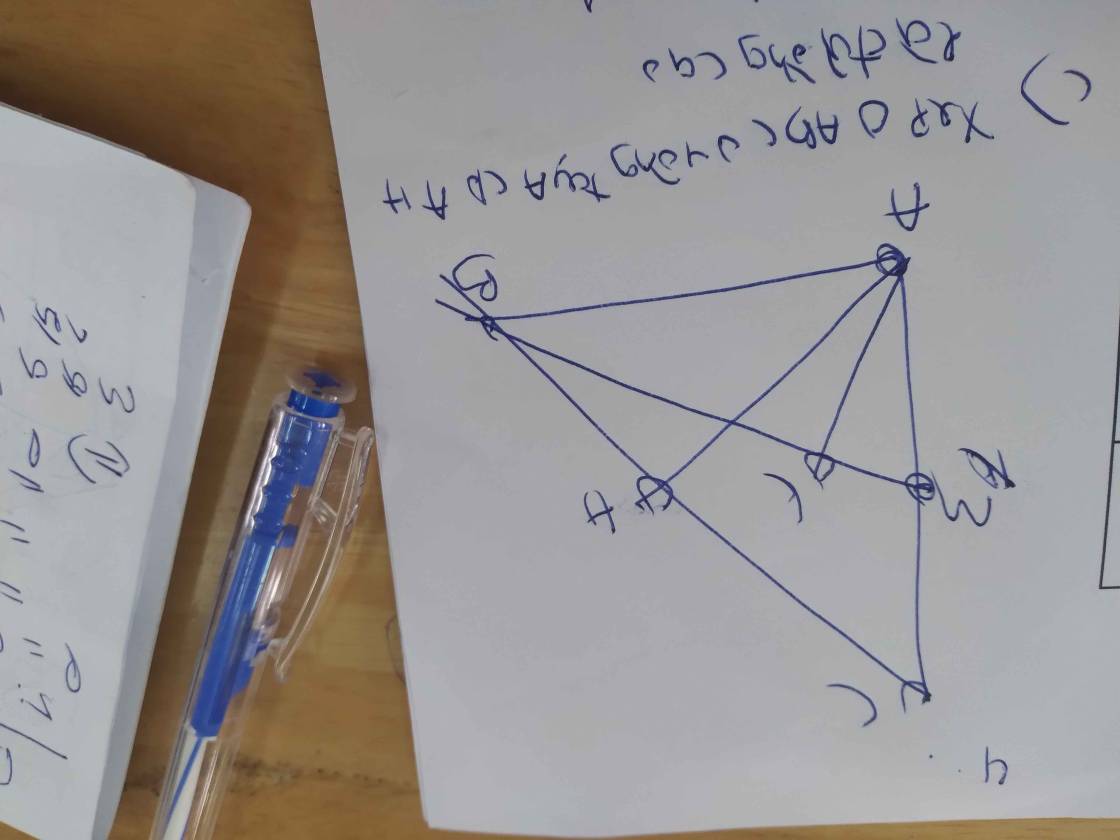
a:
Gọi O là trung điểm của AD
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó:ΔACD vuông tại C
Xét tứ giác EFDC có \(\widehat{EFD}+\widehat{ECD}=90^0+90^0=180^0\)
nên EFDC là tứ giác nội tiếp
b: Xét (O) có
\(\widehat{BCA}\) là góc nội tiếp chắn cung BA
\(\widehat{BDA}\) là góc nội tiếp chắn cung BA
Do đó: \(\widehat{BCA}=\widehat{BDA}\)
mà \(\widehat{BDA}=\widehat{ACF}\)(ECDF là tứ giác nội tiếp)
nên \(\widehat{BCA}=\widehat{ACF}\)
=>CA là phân giác của góc BCF



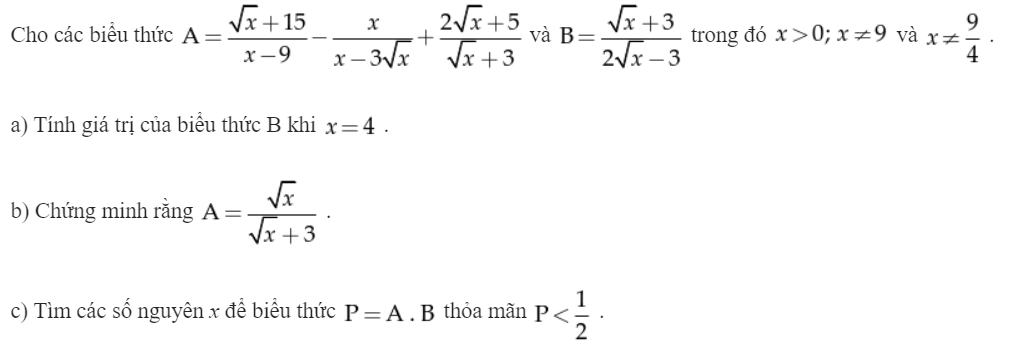
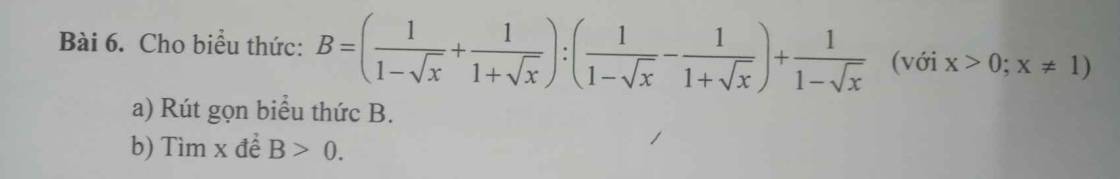 Câu (a) đã rút gọn được là
Câu (a) đã rút gọn được là