Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a. Hai góc kề bù:
$\widehat{xOy}$ và $\widehat{yOm}$
b.
Vì $\widehat{xOy}$ và $\widehat{yOm}$ kề bù nên:
$\widehat{xOy}+\widehat{yOm}=180^0$
$\widehat{yOm}=180^0-\widehat{xOy}=180^0-60^0=120^0$
c.
Vì $Om$ là phân giác $\widehat{xOy}$ nên $\widehat{yOt}=\widehat{xOt}=\frac{1}{2}\widehat{xOy}=\frac{1}{2}.60^0=30^0$
$\widehat{xOt}$ và $\widehat{tOm}$ là 2 góc kề bù nên:
$\widehat{xOt}+\widehat{tOm}=180^0$
$\widehat{tOm}=180^0-\widehat{xOt}=180^0-30^0=150^0$

Để vẽ các góc có số đo 100 độ, ta cần một cặp song song song và một cặp cạnh chéo nhau. Vì tia OZ được cho là tia đối của tia OX nên ta vẽ một đường thẳng đi qua điểm O và cắt tia OX tạo thành tia OZ. a) Trong hình vẽ trên, tên hai góc kề bù là góc xOY và góc yOZ. b) Để tính số đo góc yOZ, ta cần biết số đo góc xOY và biết rằng các góc kề bù có tổng bằng 180 độ. Vì vậy, đại lượng đo góc yOZ = 180 - đại lượng đo góc xOY. c) Để vẽ đường phân giác OT của góc xOY, ta có thể tìm trung điểm M của đoạn thẳng XY, sau đó vẽ đường thẳng đi qua đỉnh O và trung điểm M. - Để tính số đo góc TOY, ta biết rằng TOY là đường phân giác của góc xOY, nên số đo góc TOY = 0.5 * số đo góc xOY. - Để tính số đo góc TOZ, ta biết rằng TO là đường phân giác của góc xOY, nên số đo góc TOZ = 0.5 * số đo góc xOY. Mong rằng câu trả lời này đã giúp bạn hiểu và thực hiện được yêu cầu vẽ và tính toán


a) Hai góc kề bù có trên hình vừa vẽ là góc xOy và mOy
b) Vì \(\widehat {xOy} + \widehat {yOm} = 180^\circ \) (2 góc kề bù)
\(\begin{array}{l} \Rightarrow 60^\circ + \widehat {yOm} = 180^\circ \\ \Rightarrow \widehat {yOm} = 180^\circ - 60^\circ = 120^\circ \end{array}\)
c) Vì tia Ot là tia phân giác của góc xOy nên \(\widehat {xOt} = \widehat {tOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.60^\circ = 30^\circ \)
Mà \(\widehat {xOt}\) và \(\widehat {tOm}\) là hai góc kề bù nên
\(\begin{array}{l}\widehat {xOt} + \widehat {tOm} = 180^\circ \\ \Rightarrow 30^\circ + \widehat {tOm} = 180^\circ \\ \Rightarrow \widehat {tOm} = 180^\circ - 30^\circ = 150^\circ \end{array}\)
Vậy \(\widehat {tOy} = 30^\circ ;\widehat {tOm} = 150^\circ \)

`#3107`
`1,`
`a)` Yc là tính \(\widehat{yOm}\) và \(\widehat{xOn}\) phải k c? Ba điểm x, O, m cùng nằm trên 1 đt' mà?
Vì \(\widehat{xOy}\) và \(\widehat{xOn}\) là 2 góc kề bù
\(\widehat{xOy} + \widehat{xOn} = 180^0 \\ \Rightarrow 50^0 + \widehat{xOn} = 180^0 \\ \Rightarrow \widehat{xOn} = 130^0\)
Vì \(\widehat{xOn}\) và \(\widehat{yOm}\) là 2 góc đối đỉnh
`=>`$ \widehat{xOn} = \widehat{yOm} = 130^0$
Vậy, $ \widehat{xOn} = \widehat{yOm} = 130^0.$
`b)`
Vì Oz là tia phân giác của $\widehat{yOm}$
`=>` $\widehat{mOz} = \widehat{yOz} = \dfrac{1}{2} \widehat{yOm}$
`=>` $\widehat{mOz} = \dfrac{1}{2} . 130^0 = 65^0$
Vậy, $\widehat{mOz} = 65^0.$

a) các cặp góc kề bù là : góc nOx kề bù góc xOy ; góc nOm kề bù góc mOy ; góc nOm kề bù góc nOx ; góc xOy kề bù góc yOm
b) Ta có : \(\widehat{xOy}+\widehat{xOn}=180^o\) (kề bù)
50o+ góc xOn = 180o
góc xOn = 180o-50o
góc xOn = 130o
Vì Om là tia đối của Ox ; On là tia đối của Oy nên :
=> góc yOm đối đỉnh góc xOn = 130o
=> góc xOy đối đỉnh mOn = 50o
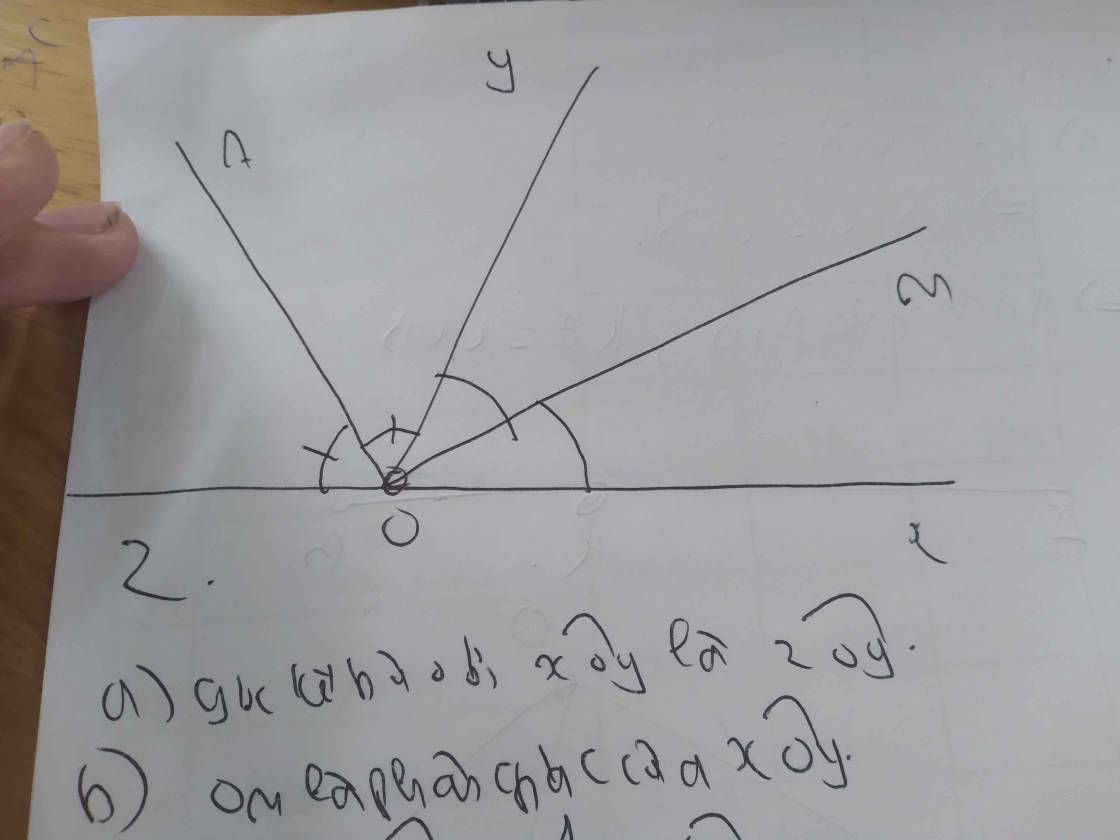

a: góc xOy và góc mOy
b: góc mOy=180-72=108 độ