a: góc CEM+góc CDM=180 độ

=>CEMD nội tiếp

b: góc EDM=góc ECM

góc FDM=góc FBM=góc ABM

=>góc EDF=góc ACM+góc ABM=60 độ

a/

D và E cùng nhìn MC dưới 1 góc vuông -> CDME là tứ giác nội tiếp

b/

CM tương tự ta cũng có tứ giác BDMF là tứ giác nội tiếp

\(\Rightarrow\widehat{MBF}=\widehat{MDF}\) (góc nt cùng chắn cung MF) (1)

Xét tứ giác nt CDME có

\(\widehat{MCE}=\widehat{MDE}\) (góc nt cùng chắn cung MF) (2)

Từ (1) và (2) \(\Rightarrow\widehat{MBF}+\widehat{MCE}=\widehat{MDF}+\widehat{MDE}=\widehat{EDF}\) (3)

Xét \(\Delta ABC\) có

AB=AC (Hai tiếp tuyến cùng xp từ 1 điểm)

=> \(\Delta ABC\) cân tại A \(\Rightarrow\widehat{ABC}=\widehat{ACB}=\dfrac{180^o-\widehat{xAy}}{2}=\dfrac{180^o-60^o}{2}=60^o\)

Ta có

\(sđ\widehat{ABC}=\dfrac{1}{2}sđ\) cung BC => sđ cung BC = 2.sđ \(\widehat{ABC}=2.60^o=120^o\) 

=> sđ cung BM + sđ cung CM = sđ cung BC \(=120^o\)

Ta có

\(sđ\widehat{MBF}=\dfrac{1}{2}sđ\)  cung BM (góc giữa tiếp tuyến và dây cung)

\(sđ\widehat{MCE}=\dfrac{1}{2}sđ\) cung CM (góc giữa tiếp tuyến và dây cung)

\(\Rightarrow sđ\widehat{MBF}+sđ\widehat{MCE}=sđ\widehat{EDF}=\dfrac{sđcungBM+sđcungCM}{2}=\dfrac{sđcungBC}{2}=\dfrac{120^0}{2}=60^o\)

c/

Xét tg vuông MBF và tg vuông MCD có

\(sđ\widehat{MBF}=\dfrac{1}{2}sđcungBM\) (góc giữa tiếp tuyến và dây cung)

\(sđ\widehat{MCD}=\dfrac{1}{2}sđcungBM\) (góc nt)

\(\Rightarrow\widehat{MBF}=\widehat{MCD}\) => tg MBF đồng dạng với tg MCD

\(\Rightarrow\dfrac{MF}{MD}=\dfrac{MB}{MC}\)

CM tương tự ta cũng có tg vuông MCE đồng dạng với tg vuông MBD

\(\Rightarrow\dfrac{ME}{MD}=\dfrac{MC}{MB}\Rightarrow\dfrac{MD}{ME}=\dfrac{MB}{MC}\)

\(\Rightarrow\dfrac{MF}{MD}=\dfrac{MD}{ME}\Rightarrow MD^2=ME.MF\left(đpcm\right)\)

a. Vì \(CE\perp MA\)tại E (gt) => \(\widehat{AEC}=90^o\)

\(CD\perp AB\)tại D=> \(\widehat{ADC}=90^o\)

Xét tứ giác AECD có: \(\widehat{AEC}+\widehat{ADC}=90^o+90^o=180^o\)=> AECD là tứ giác nội tiếp đt \((G,R=\frac{AC}{2})\)trong đó G là trung điểm của AC (dhnb)

Cmtt ta có: BFCD là tứ giác nội tiếp đt \((H,R=\frac{BC}{2})\)trong đó H là trung điểm của BC

b. 

Vì AECD là tứ giác nội tiếp (cmt) => \(\widehat{EAC}=\widehat{EDC}\)(2 góc nội tiếp cùng chắn \(\widebat{EC}\)) (1)

Do MA là tiếp tuyến của đt(O) (gt)=> \(\widehat{EAC}=\frac{1}{2}sđ\widebat{AC}\)(t/c góc tạo bởi tiếp tuyến và dây cung)

Xét đt (O) có: \(\widehat{ABC}=\widehat{DBC}=\frac{1}{2}sđ\widebat{AC}\)(t/c góc nội tiếp) => \(\widehat{EAC}=\widehat{DBC}\)(2)

vì BFCD là tứ giác nội tiếp => \(\widehat{DBC}=\widehat{DFC}\)(2 góc nội tiếp cùng chắn \(\widebat{DC}\)) (3)

Từ (1),(2) và (3) => \(\widehat{EDC}=\widehat{DFC}\)

do AECD là tứ giác nội tiếp (cmt) => \(\widehat{CED}=\widehat{CAD}\)(2 góc nội tiếp cùng chắn \(\widebat{CD}\)) (4)

Vì MB là tiếp tuyến của đt (O) tại B (gt) => \(\widehat{CBF}=\frac{1}{2}sđ\widebat{BC}\)(T/c góc tạo bởi tiếp tuyến và dây cung)

Xét đt (O) có: \(\widehat{BAC}=\widehat{DAC}=\frac{1}{2}sđ\widebat{BC}\)(t/c góc nội tiếp) => \(\widehat{CBF}=\widehat{DAC}\)(5)

lại có: BFCD là tứ giác nội tiếp (cmt) => \(\widehat{CBF}=\widehat{CDF}\)(2 góc nội tiếp cùng chắn \(\widebat{CF}\)) (6)

Từ (4), (5) và (6) => \(\widehat{CED}=\widehat{CDF}\)

Xét \(\Delta ECD\)và \(\Delta DCF\)có:

\(\widehat{CED}=\widehat{CDF}\)(Cmt)

\(\widehat{EDC}=\widehat{DFC}\)(Cmt)

=> \(\Delta ECD~\Delta DCF\)(g.g) => \(\frac{EC}{DC}=\frac{CD}{CF}\Rightarrow CD^2=CE\times CF\)(Đpcm)

c. Vì I là giao điểm của AC và DE (gt) => \(I\in AC\)

K là giao điểm của BC và DF (gt) => \(K\in BC\)

=> \(\widehat{ICK}=\widehat{ACB}\)

Vì \(\widehat{EDC}=\widehat{ABC}\left(cmt\right)\Rightarrow\widehat{IDC}=\widehat{ABC}\left(do\overline{E,I,D}\Rightarrow\widehat{EDC}=\widehat{IDC}\right)\)

\(\widehat{CDF}=\widehat{BAC}\left(cmt\right)\Rightarrow\widehat{CDK}=\widehat{BAC}\left(do\overline{F,K,D}\Rightarrow\widehat{CDF}=\widehat{CDK}\right)\)

Xét tứ giác ICKD có : \(\widehat{ICK}+\widehat{IDK}=\widehat{ICK}+\widehat{IDC}+\widehat{CDK}=\widehat{ACB}+\widehat{ABC}+\widehat{BAC}=180^o\)

(Áp dụng định lý tổng 3 góc trong \(\Delta ABC\)ta có: \(\widehat{ACB}+\widehat{ABC}+\widehat{BAC}=180^o\))

=> Tứ giác ICKD là tứ giác nội tiếp (dhnb) => 4 điểm I,C,K,D cùng thuộc 1 đường tròn (đpcm)

d. Vì ICKD là tứ giác nội tiếp (cmt) => \(\widehat{CIK}=\widehat{CDK}\)(2 góc nội tiếp cùng chắn \(\widebat{CK}\))

Lại có: \(\widehat{CDK}=\widehat{BAC}\)(Cmt)  => \(\widehat{CIK}=\widehat{BAC}\)mà 2 góc này ở vị tri đồng vị => IK // AB (Dhnb)

Do \(CD\perp AB\left(gt\right)\)=> \(IK\perp CD\)(Quan hệ tính vuông góc và tính song song của 3 đt)

Bạn cho mình hỏi ở phần nào đk ?

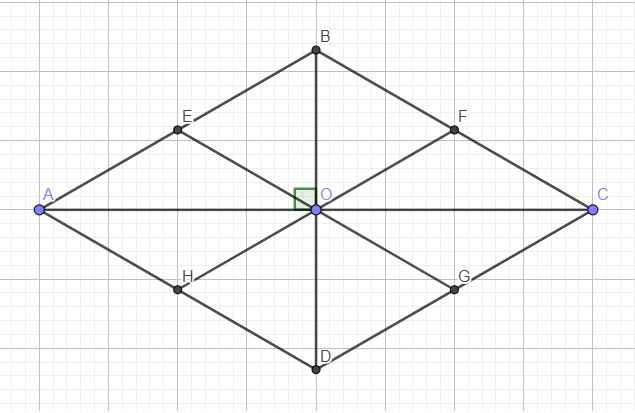
Do ABCD là hình thoi \(\Rightarrow\Delta BCD\) cân tại C

Mà \(C=60^0\Rightarrow\Delta BCD\) đều

Hoàn toàn tương tự, ta có tam giác ABD đều

\(\Rightarrow AB=BC=CD=DA=BD\) (1)

Gọi O là giao điểm 2 đường chéo \(\Rightarrow OA\perp OB\)

Trong tam giác vuông OAB, do E là trung điểm AB nên OE là trung tuyến ứng với cạnh huyền

\(\Rightarrow OE=\dfrac{1}{2}AB\) (2)

Mà O là trung điểm BD (tính chất hình thoi) \(\Rightarrow OB=\dfrac{1}{2}BD\) (3)

(1);(2);(3) \(\Rightarrow OE=OB\)

Hoàn toàn tương tự, ta có: 

\(OE=OB=OF=OG=OD=OH\)

\(\Rightarrow\) Các điểm E, B, F, G, D, H cùng thuộc 1 đường tròn tâm O bán kính OB