Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

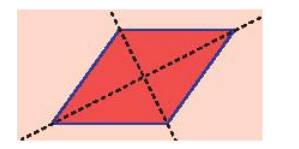
+) Trục đối xứng của hình thoi là đường chéo vì nếu gấp hình theo đường chéo thì hai tam giác đó chồng khít lên nhau

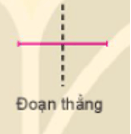
1. Thực hành gấp giấy: Vẽ đoạn thẳng trên tờ giấy, gấp tờ giấy theo một đường thẳng sao cho 2 đầu đoạn thẳng trùng nhau thì đường thẳng đó là một trục đối xứng.
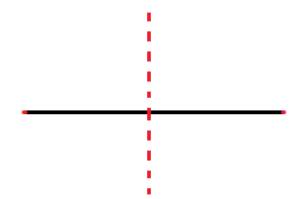
+) Trục đối xứng của đoạn thẳng là đường thẳng thu được khi gấp giấy.
2.
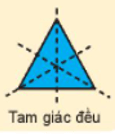
+) Trục đối xứng của tam giác đều là đường thẳng nối đỉnh của tam giác với trung điểm cạnh đối diện (có 3 trục đối xứng)
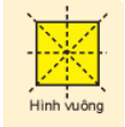
+) Trục đối xứng của hình vuông là đường chéo của hình vuông và hai đường thẳng đi qua trung điểm từng cặp cạnh đối diện của hình vuông (có 4 trục đối xứng)
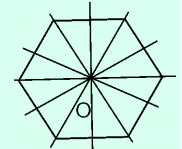
+) Trục đối xứng của lục giác đều là đường thẳng nối 1 đỉnh và tâm của lục giác đều (có 6 trục đối xứng).
a) Trục đối xứng của đoạn thẳng là đường thẳng thu được khi gấp giấy.
b)
+ Tam giác đều có 3 trục đối xứng là đường thẳng nối đỉnh của tam giác với trung điểm cạnh đối diện
+ Hình vuông có 4 trục đối xứng là đường chéo của hình vuông và hai đường thẳng đi qua trung điểm từng cặp cạnh đối diện của hình vuông
+ Hình lục giác đều có 6 trục đối xứng.

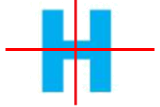
1. Những hình có trục đối xứng là: A, H, E
+ Chữ A có một trục đối xứng như sau:

+ Chữ H có 2 trục đối xứng:
+ Chữ E có 1 trục đối xứng:

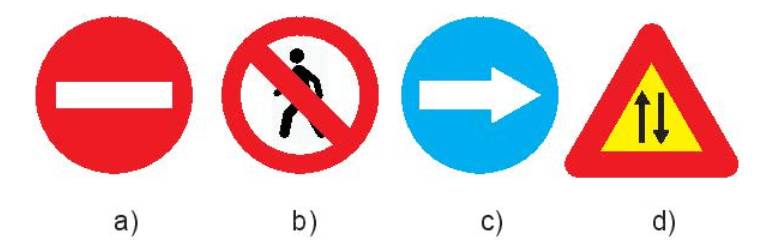
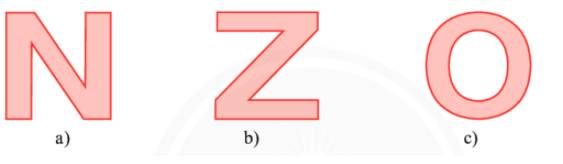
2. Những hình có trục đối xứng là: a) và c)
+) Với biển báo a) “cấm đi ngược chiều”: trục đối xứng là đường thẳng đứng và đường nằm ngang đi qua tâm của biển báo.

+) Với biển báo c) “chỉ hướng phải đi theo”: trục đối xứng là đường nằm ngang đi qua tâm của biển báo.

3. Một số ví dụ về hình có trục đối xứng: mặt bàn, cái mâm, viên bi, chiếc bảng, khung cửa sổ, …
Các chữ cái: I, O, M, số 0, số 8,….có trục đối xứng.
Minh họa bằng 1 hình ảnh có trục đối xứng:


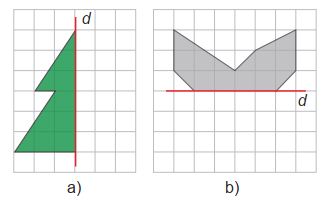
Hình a , b không có trục đối xứng.
Hình c có vô số trục đối xứng.
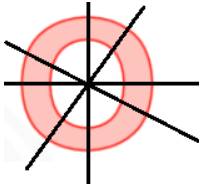


Vẽ hơi xấu nhưng có lẽ dạng dạng giống như vậy ạ!!!
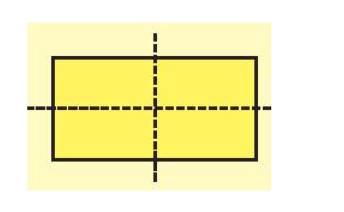

+) Trục đối xứng của hình chữ nhật là đường thẳng đi qua trung điểm hai cạnh đối diện vì khi gấp theo đường đó thì ta được hai hình chữ nhật chồng khít lên nhau.
+) Ta tìm được hai trục đối xứng.