Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{-5}{6}=\dfrac{-5\times4}{6\times4}=\dfrac{-20}{24}\)
\(\dfrac{3}{-8}=\dfrac{3\times\left(-3\right)}{-8\times\left(-3\right)}=\dfrac{-9}{24}\)
\(2=\dfrac{48}{24}\)
\(\dfrac{-25}{100}=\dfrac{-1}{4}=\dfrac{-1\times6}{4\times6}=\dfrac{-6}{24}\)
\(\dfrac{72}{108}=\dfrac{2}{3}=\dfrac{2\times8}{3\times8}=\dfrac{16}{24}\)

a) \(\dfrac{2}{5}=\dfrac{1}{5}\cdot\dfrac{2}{1}\)
\(\dfrac{15}{12}=\dfrac{5}{4}=\dfrac{5}{2}\cdot\dfrac{1}{2}\)
\(\dfrac{5}{-12}=\dfrac{-5}{12}=\dfrac{-5}{3}\cdot\dfrac{1}{4}\)
\(\dfrac{-3}{-4}=\dfrac{3}{4}=\dfrac{3}{2}\cdot\dfrac{1}{2}\)

a) \(\dfrac{1}{6};\dfrac{1}{3};\dfrac{1}{2};...\)
\(\Rightarrow\dfrac{1}{6};\dfrac{2}{6};\dfrac{3}{6};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{4}{6}\)
b) \(\dfrac{1}{8};\dfrac{5}{24};\dfrac{7}{24};...\)
\(\Rightarrow\dfrac{3}{24};\dfrac{5}{24};\dfrac{7}{24};...\)
Dãy có quy luật tăng dần lên 2 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{9}{24}\)
c) \(\dfrac{1}{5};\dfrac{1}{4};\dfrac{1}{3};...\)
\(\dfrac{4}{20};\dfrac{5}{20};\dfrac{6}{20};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{7}{20}\)
d) \(\dfrac{4}{15};\dfrac{3}{10};\dfrac{1}{3};...\)
\(\Rightarrow\dfrac{8}{30};\dfrac{9}{30};\dfrac{11}{30};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{12}{30}\)

26/65= 0,4
45/-250 = -0,18
2 3/8= 2,375
36/-400= -0,09
1 469/2000= 1,2345

a) \(\left\{{}\begin{matrix}\dfrac{1}{5}=\dfrac{1.6}{5.6}=\dfrac{6}{30}\\\dfrac{1}{6}=\dfrac{1.5}{6.5}=\dfrac{5}{30}\\\dfrac{2}{15}=\dfrac{2.2}{15.2}=\dfrac{4}{30}\\\dfrac{1}{10}=\dfrac{1.3}{10.3}=\dfrac{3}{30}\end{matrix}\right.\)
Quy luật: Tử số của mỗi phân số cách nhau \(1\) đơn vị, cùng chung mẫu số là \(30\).
Phân số tiếp theo: \(\dfrac{2}{30}=\dfrac{1}{15}\)
b) \(\left\{{}\begin{matrix}\dfrac{1}{9}=\dfrac{1.5}{9.5}=\dfrac{5}{45}\\\dfrac{1}{15}=\dfrac{1.3}{15.3}=\dfrac{3}{45}\end{matrix}\right.\)
Quy luật: Tử số của mỗi phân số cách nhau \(1\) đơn vị, cùng chung mẫu số là \(45\).
Phân số tiếp theo: \(\dfrac{1}{45}\)


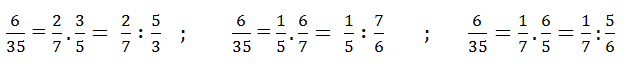

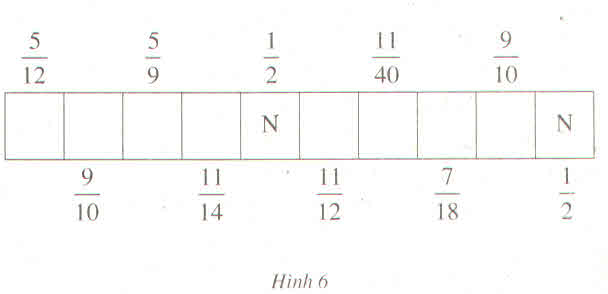
 Đó là hai địa danh HỘI AN và MỸ SƠN của Viêt Nam được UNESCO công nhân là di sản văn hóa thế giới vào năm 1999.
Đó là hai địa danh HỘI AN và MỸ SƠN của Viêt Nam được UNESCO công nhân là di sản văn hóa thế giới vào năm 1999.
\(\dfrac{-1}{3}=\dfrac{-12}{36}\)
\(\dfrac{2}{3}=\dfrac{24}{36}\)
\(\dfrac{-1}{-2}=\dfrac{1}{2}=\dfrac{18}{36}\)
\(\dfrac{6}{-24}=\dfrac{-1}{4}=\dfrac{-9}{36}\)
\(\dfrac{-3}{4}=\dfrac{-27}{36}\)
\(\dfrac{10}{60}=\dfrac{1}{6}=\dfrac{6}{36}\)
\(\dfrac{-5}{6}=\dfrac{-30}{36}\)