a: Vì (d)//(d') nên \(a=-\dfrac{2}{3}\)

Vậy: \(\left(d\right):y=-\dfrac{2}{3}x+b\)

Thay x=4 và y=-3 vào (d), ta được:

\(-\dfrac{2}{3}\cdot4+b=-3\)

\(\Leftrightarrow b=-3+\dfrac{8}{3}=-\dfrac{1}{3}\)

b: Vì (d) vuông góc với (d') nên \(\dfrac{1}{3}a=-1\)

hay a=-3

vậy: (d): y=-3x+b

Thay x=2 và y=3 vào (d), ta được:

b-6=3

hay b=9

Tớ làm mẫu câu a nhé: 

Phương trình hoành độ giao điểm của (d₁) và (d₂) là:

\(3x=-x+4\Leftrightarrow4x=4\Leftrightarrow x=1\)

\(\Rightarrow y=3x=3.1=3\)

Vậy tọa độ giao điểm của (d₁) và (d₂) là (1;3)

Câu b cách làm tương tự câu a, riêng câu c thì bạn phải viết y theo x (nghĩa là để lại y ở một vế (vế trái) và chuyển hết sang vế kia (vế phải), làm như vậy với cả hai phương trình. Sau khi đã rút được y theo x rồi thì áp dụng cách làm như câu a.

a) Vì (d): y=ax+b//y=3x+1 nên \(\left\{{}\begin{matrix}a=3\\b\ne1\end{matrix}\right.\)

Suy ra: (d): y=3x+b

Thay x=2 và y=-2 vào (d), ta được:

\(3\cdot2+b=-2\)

\(\Leftrightarrow b=-8\)(thỏa ĐK)

Vậy: (d): y=3x-8

b) Để (d) vuông góc với y=2x+3 nên \(2a=-1\)

hay \(a=-\dfrac{1}{2}\)

Vậy: (d): \(y=\dfrac{-1}{2}x+b\)

Thay x=-3 và y=4 vào (d), ta được:

\(\dfrac{-1}{2}\cdot\left(-3\right)+b=4\)

\(\Leftrightarrow b+\dfrac{3}{2}=4\)

hay \(b=\dfrac{5}{2}\)

Vậy: (d): \(y=\dfrac{-1}{2}x+\dfrac{5}{2}\)

PT của đường thẳng cần tìm có dạng: `(d): y=ax+b `

`(d)` vuông góc `(d') : y=1/3 x-7/3 <=> a. 1/3 = -1 <=> a=-3`

`=> y=-3x+b`

`A (0;4) \in (d) <=> 4=-3.0+b <=> b=4`

`=> y=-3a+4`.

a. Em tự giải

b. Từ giả thiết ta có \(A\left(-2;1\right)\) và \(B\left(4;4\right)\)

Gọi phương trình (d) có dạng \(y=ax+b\), do (d) qua A và B nên:

\(\left\{{}\begin{matrix}-2a+b=1\\4a+b=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=2\end{matrix}\right.\) \(\Rightarrow y=\dfrac{1}{2}x+2\)

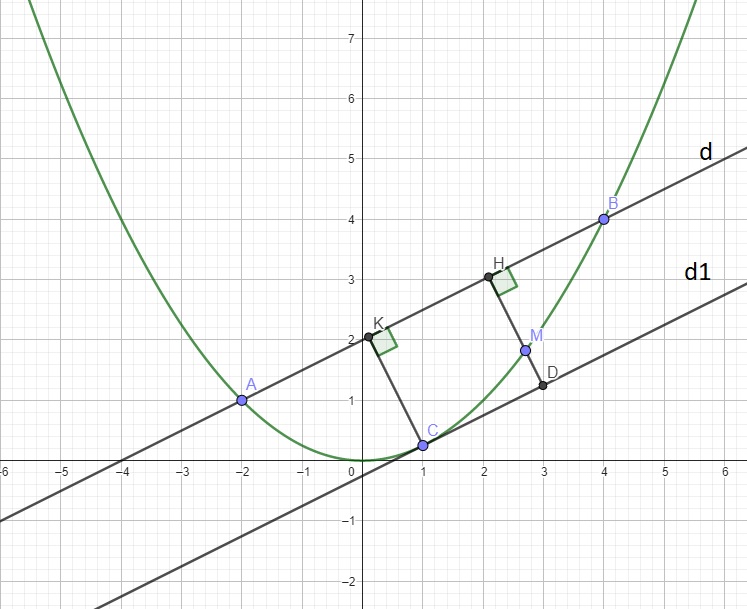
c. Câu này có vài cách giải cho lớp 9, cách nhanh nhất là sử dụng tính chất tiếp tuyến.

Từ M kẻ \(MH\perp AB\Rightarrow S_{ABM}=\dfrac{1}{2}MH.AB\)

Do AB cố định \(\Rightarrow S_{max}\) khi \(MH_{max}\)

Gọi \(d_1\) là đường thẳng song song d và tiếp xúc (P), gọi C là tiếp điểm \(d_1\) và (P)

Do \(d_1\) song song (d) nên pt có dạng: \(y=\dfrac{1}{2}x+b\)

Phương trình hoành độ giao điểm \(d_1\) và (P):

\(\dfrac{1}{4}x^2=\dfrac{1}{2}x+b\Rightarrow x^2-2x-4b=0\) (1)

Do \(d_1\) tiếp xúc (P) \(\Rightarrow\left(1\right)\) có nghiệm kép

\(\Rightarrow\Delta'=1+4b=0\Rightarrow b=-\dfrac{1}{4}\)

Thế vào (1) \(\Rightarrow x_C^2-2x_C+1=0\Rightarrow x_C=1\Rightarrow y_C=\dfrac{1}{4}\) \(\Rightarrow C\left(1;\dfrac{1}{4}\right)\)

Từ C kẻ \(CK\perp d\)

Giả sử HM kéo dài cắt \(d_1\) tại D \(\Rightarrow\) tứ giác CKHD là hình chữ nhật (2 cặp cạnh đối song song và 1 góc vuông)

\(\Rightarrow CK=DH\)

Mà \(DH=MH+MD\ge MH\Rightarrow CK\ge MH\)

\(\Rightarrow MH_{max}=CK\) khi M trùng C

Hay \(M\left(1;\dfrac{1}{4}\right)\)

Ta có:

\(\left(d\right):y=2mx+m-1\) qua \(M\left(-1;4\right)\), thay \(x=-1,y=4\) vào đồ thị được: 

\(2.m.\left(-1\right)+m-1=4\\ \Rightarrow m=-5\)

Pt có dạng: \(y=-10x-6\)

Vậy (d) không song song với đường thẳng \(y=1-5x\) vì hệ số a khác nhau ( \(-10\ne-5\) )

b. Hệ pt tương đương với \(\left\{{}\begin{matrix}-7x+3y=5\\-7x+7y=-7\end{matrix}\right.\)

\(\Rightarrow-4y=12\\ \Rightarrow y=-3\\ \Rightarrow x=-2\)

Vậy hệ phương trình có tập nghiệm \(S=\left(x;y\right)=\left(-2;-3\right)\)

a) Gọi (d): y=ax+b

Vì (d)//y=2x-3 nên \(\left\{{}\begin{matrix}a=2\\b\ne-3\end{matrix}\right.\)

Vậy: (d): y=2x+b

Vì (d) đi qua điểm C(-1;4) nên 

Thay x=-1 và y=4 vào (d), ta được:

\(2\cdot\left(-1\right)+b=4\)

hay b=6

Vậy: (d): y=2x+6

Thay y=0 vào (d), ta được:

2x+6=0

hay x=-3

Vậy: A(-3;0)

b) Vì y=ax+b đi qua hai điểm B(4;0) và C(-1;4) nên ta có hệ phương trình:

\(\left\{{}\begin{matrix}4a+b=0\\-a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5a=-4\\b=a+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{4}{5}\\b=\dfrac{-4}{5}+4=\dfrac{-4}{5}+\dfrac{20}{5}=\dfrac{16}{5}\end{matrix}\right.\)

Tính góc tạo bởi đường thẳng BC và trục hoành Ox đi