
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Những phương trình là phương trình chính tắc của (H) là: b), c), d).

Chọn D.
Ta có: ± b a = ± 2 3 ⇒ a = 3 b = 2 .
Phương trình (H) : x 2 9 - y 2 4 = 1

Đáp án: D
Hypebol có hai đường tiệm cận
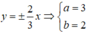
Vậy phương trình của hypebol là:
x 2 9 - y 2 4 = 1
Viết phương trình các parabol sau đây dưới dạng chính tắc:
a) \(x = \frac{{{y^2}}}{4}\)
b) \(x-y^2=0\)

a) \(x = \frac{{{y^2}}}{4} \Leftrightarrow {y^2} = 4x\)
Vậy dạng chính tắc của parabol là: \({y^2} = 4x\)
b) \(x - {y^2} = 0 \Leftrightarrow {y^2} = x\)
Vậy dạng chính tắc của parabol là: \({y^2} = x\)

a) Đây là một parabol. Tiêu điểm của parabol có tọa độ là: \(F\left({\frac{9}{2};0} \right)\).
b) Đây là một elip. Tiêu điểm của elip có tọa độ là: \(\left\{ \begin{array}{l}{F_1}\left( { - \sqrt {{a^2} - {b^2}} ;0} \right) = \left( { - \sqrt {39} ;0} \right)\\{F_2}\left( {\sqrt {{a^2} - {b^2}} ;0} \right) = \left( {\sqrt {39} ;0} \right)\end{array} \right.\)
c) Đây là một hyperbol. Tiêu điểm của hypebol có tọa độ là: \(\left\{ \begin{array}{l}{F_1}\left( { - \sqrt {{a^2} + {b^2}} ;0} \right) = \left( { - 5;0} \right)\\{F_2}\left( {\sqrt {{a^2} + {b^2}} ;0} \right) = \left( {5;0} \right)\end{array} \right.\)

a) Ta thấy phương trình có dạng \(a{x^2} + b{y^2} = 1\) nên phương trình \(({C_1}):4{x^2} + 16{y^2} = 1\) là phương trình của đường elip
Từ phương trình \(({C_1}):4{x^2} + 16{y^2} = 1\) ta có phương trình chính tắc là \(({C_1}):\frac{{{x^2}}}{{\frac{1}{4}}} + \frac{{{y^2}}}{{\frac{1}{{16}}}} = 1\)
Từ phương trình chính tắc ta có: \(a = \frac{1}{2},b = \frac{1}{4} \Rightarrow c = \sqrt {{a^2} - {b^2}} = \sqrt {{{\left( {\frac{1}{2}} \right)}^2} - {{\left( {\frac{1}{4}} \right)}^2}} = \frac{{\sqrt 3 }}{4}\)
Suy ra tiêu điểm của elip này là \({F_1}\left( { - \frac{{\sqrt 3 }}{4};0} \right)\) và \({F_2}\left( {\frac{{\sqrt 3 }}{4};0} \right)\)
b) Ta thấy phương trình có dạng \(a{x^2} - b{y^2} = 1\) nên phương trình \(({C_2}):16{x^2} - 4{y^2} = 144\) là phương trình của đường hypebol
Từ phương trình \(({C_2}):16{x^2} - 4{y^2} = 144\) ta có phương trình chính tắc là \(({C_1}):\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{36}} = 1\)
Từ phương trình chính tắc ta có: \(a = 3,b = 6 \Rightarrow c = \sqrt {{a^2} + {b^2}} = \sqrt {{3^2} + {6^2}} = 3\sqrt 5 \)
Suy ra tiêu điểm của hypebol này là \({F_1}\left( { - 3\sqrt 5;0} \right)\) và \({F_2}\left( {3\sqrt 5;0} \right)\)
c) Phương trình \(({C_3}):x = \frac{1}{8}{y^2}\) có dạng \({y^2} = ax\) nên phương trình này là phương trình của parabol
Ta có phương trình chính tắc là \({y^2} = 8x\)
Từ phương trình chính tắc ta có: \(2p = 8 \Rightarrow p = 4\)
Suy ra tiêu điểm là \(F(2;0)\)

Ta có: \(2c = 10 \Rightarrow c = 5,2b = 6 \Rightarrow b = 3\)
Suy ra \(a = \sqrt {{c^2} - {b^2}} = \sqrt {{5^2} - {3^2}} = 4\)
Vậy phương trình chính tắc của hypebol có dạng \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\)
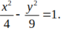
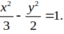
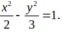
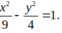
Ta có: \(4{x^2}-9{y^2} = {\rm{ }}1 \Leftrightarrow \frac{{{x^2}}}{{{{\left( {\frac{1}{4}} \right)}^2}}} - \frac{{{y^2}}}{{{{\left( {\frac{1}{9}} \right)}^2}}} = 1\)
Vậy phương trình chính tắc của hypebol là: \(\frac{{{x^2}}}{{{{\left( {\frac{1}{4}} \right)}^2}}} - \frac{{{y^2}}}{{{{\left( {\frac{1}{9}} \right)}^2}}} = 1\)