
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


#)Giải :
Ta có : \(4a^2b^2-\left(a^2+b^2-c^2\right)^2\)
\(=4a^2b^2-\left(a^4+b^4+c^4+2a^2b^2-2b^2c^2-2c^2a^2\right)\)
\(=4a^2b^2-a^4-b^4-c^4-2a^2b^2+2b^2c^2+2c^2a^2\)
\(=2a^2b^2-a^4-b^4-c^4+2b^2c^2+2c^2a^2\)
\(=-a^4+2a^2b^2-b^4-c^2+2b^2c^2+2c^2a^2\)
\(=-\left(a^2-b^2\right)^2-c^4+2b^2c^2+2c^2c^2\)
\(=-\left(a^2-b^2\right)^2-c\left(c^2-2b^2+2a^2\right)>0\)
\(\Rightarrow A>0\left(đpcm\right)\)
\(A=\left(2ab+a^2+b^2-c^2\right)\left(2ab-a^2-b^2+c^2\right)\)
=>\(A=\left(a+b-c\right)\left(a+b+c\right)\left(c-a+b\right)\left(a-b+c\right)\)
do a,b,c la do dai 3 canh tam giac => A>0=>dpcm



Đặt \(A=\sqrt{a+1}+\sqrt{a+3}\)
\(\Rightarrow A^2=2a+4+2\sqrt{\left(a+1\right)\left(a+3\right)}\)
Đặt \(B=2\sqrt{a+2}\)
\(\Rightarrow B^2=4a+8\)
Xét hiệu \(B^2-A^2=2a+4-2\sqrt{\left(a+1\right)\left(a+3\right)}\)
Áp dụng BĐT Cô-si, ta có \(2a+4=\left(a+1\right)+\left(a+3\right)\) \(>2\sqrt{\left(a+1\right)\left(a+3\right)}\)
(Dấu "=" không thể xảy ra vì khi đó sẽ suy ra đẳng thức vô lí là \(1=3\))
Từ đó suy ra \(B^2-A^2>0\) \(\Leftrightarrow B^2>A^2\), và do A, B dương nên suy ra \(B>A\). Nói cách khác, \(2\sqrt{a+2}>\sqrt{a+1}+\sqrt{a+3}\)
sao em bấm máy tính thì dấu bằng ảy ra khi =10000000 vậy ạ.

a) ĐK: \(0< a< 1\)
\(Q=\left(\frac{\sqrt{1+a}}{\sqrt{1+a}-\sqrt{1-a}}+\frac{1-a}{\sqrt{1-a^2}-1+a}\right)\left(\sqrt{\frac{1}{a^2}-1}-\frac{1}{a}\right)\sqrt{a^2-2a+1}\)
\(=\left(\frac{\sqrt{1+a}}{\sqrt{1+a}-\sqrt{1-a}}+\frac{1-a}{\sqrt{1-a}\left(\sqrt{1+a}-\sqrt{1-a}\right)}\right)\left(\frac{\sqrt{1-a^2}}{a}-\frac{1}{a}\right).\sqrt{\left(1-a\right)^2}\)
\(=\left(\frac{\sqrt{1+a}}{\sqrt{1+a}-\sqrt{1-a}}+\frac{\sqrt{1-a}}{\sqrt{1+a}-\sqrt{1-a}}\right).\frac{\sqrt{1-a^2}-1}{a}.\left(1-a\right)\)
\(=\frac{\left(\sqrt{1+a}+\sqrt{1-a}\right)^2}{\left(\sqrt{1+a}-\sqrt{1-a}\right)\left(\sqrt{1+a}+\sqrt{1-a}\right)}.\frac{\sqrt{1-a^2}-1}{a}.\left(1-a\right)\)
\(=\frac{2+2\sqrt{1-a^2}}{2a}.\frac{\sqrt{1-a^2}-1}{a}.\left(1-a\right)\)
\(=\frac{\sqrt{1-a^2}+1}{a}.\frac{\sqrt{1-a^2}-1}{a}.\left(1-a\right)\)
\(=\frac{-a^2\left(1-a\right)}{a^2}=a-1\)
\(Q=\left(\frac{\sqrt{1+a}}{\sqrt{1+a}-\sqrt{1-a}}+\frac{1-a}{\sqrt{1-a^2}-1+a}\right)\left(\sqrt{\frac{1}{a^2}-1}-\frac{1}{a}\right)\sqrt{a^2-2a+1}\)
\(=\left(\frac{\sqrt{1+a}}{\sqrt{1+a}-\sqrt{1-a}}+\frac{1-a}{\sqrt{1-a}\left(\sqrt{1+a}-\sqrt{1-a}\right)}\right)\left(\frac{\sqrt{1-a^2}}{a}-\frac{1}{a}\right).\sqrt{\left(1-a\right)^2}\)
\(=\left(\frac{\sqrt{1+a}}{\sqrt{1+a}-\sqrt{1-a}}+\frac{\sqrt{1-a}}{\sqrt{1+a}-\sqrt{1-a}}\right).\frac{\sqrt{1-a^2}-1}{a}.\left(1-a\right)\)
\(=\frac{\sqrt{1+a}+\sqrt{1-a}}{\sqrt{1+a}-\sqrt{1-a}}.\frac{\sqrt{1-a^2}-1}{a}.\left(1-a\right)\)
\(=\frac{2+2\sqrt{1-a^2}}{2a}.\frac{\sqrt{1-a^2}-1}{a}.\left(1-a\right)\)
\(=\frac{\sqrt{1-a^2}+1}{a}.\frac{\sqrt{1-a^2}-1}{a}.\left(1-a\right)\)
\(=\frac{-a^2\left(1-a\right)}{a^2}=a-1\)
b) Xét: \(Q^3-Q=\left(a-1\right)^3-\left(a-1\right)=\left(a-1\right)^2\left(a-1-1\right)=\left(a-1\right)^2\left(a-2\right)\)
Do \(a< 1\)=> \(a-2< 0\) và \(a-1< 0\)
nên \(\left(a-1\right)^2\left(a-2\right)< 0\)
=> \(Q^3-Q< 0\)
<=> \(Q^3< Q\)

a) \(\sqrt{\dfrac{2a}{3}}\cdot\sqrt{\dfrac{3a}{8}}\)
\(=\sqrt{\dfrac{2a\cdot3a}{3\cdot8}}\)
\(=\sqrt{\dfrac{6a^2}{24}}\)
\(=\sqrt{\dfrac{a^2}{4}}\)
\(=\dfrac{\sqrt{a^2}}{\sqrt{4}}\)
\(=\dfrac{a}{2}\)
b) \(\sqrt{3a}\cdot\sqrt{\dfrac{52}{a}}\)
\(=\sqrt{3a\cdot\dfrac{52}{a}}\)
\(=\sqrt{3\cdot52}\)
\(=\sqrt{13\cdot3\cdot4}\)
\(=2\sqrt{39}\)
c) \(2y^2\cdot\sqrt{\dfrac{x^4}{4y^2}}\)
\(=2y^2\cdot\dfrac{\sqrt{\left(x^2\right)^2}}{\sqrt{\left(2y\right)^2}}\)
\(=2y^2\cdot\dfrac{x^2}{-2y}\)
\(=\dfrac{2y^2\cdot x^2}{-2y}\)
\(=-x^2y\)
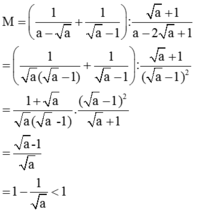
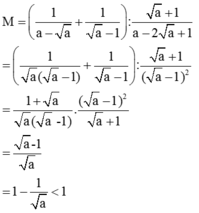
\(a^4-2a^3+a^2\)
\(=a^2\left(a^2-2a+1\right)\)
\(=a^2\left(a-1\right)^2\ge0\)
Vậy \(a^4-2a^3+a^2\ge0\)