
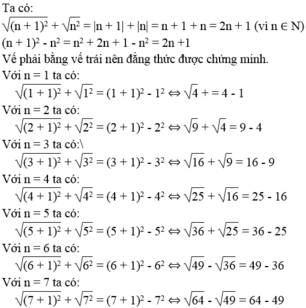
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

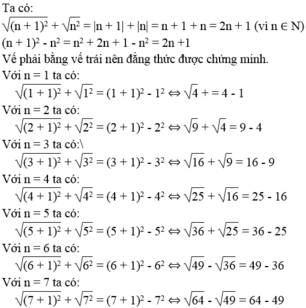

Ta có:
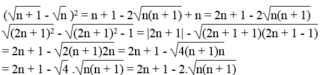
Vế trái bằng vế phải nên đẳng thức được chứng minh.
* Với n = 1, ta có: 2 - 1 2 = 9 - 8
* Với n = 2, ta có: 3 - 2 2 = 25 - 24
* Với n = 3, ta có: 4 - 3 2 = 49 - 48
* Với n = 4, ta có: 5 - 4 2 = 81 - 80

\(\sqrt{\left(n+1\right)^2}+\sqrt{n^2}=\left(n+1\right)+n=2n+1=\left(n+1-n\right)\left(n+1+n\right)=\left(n+1\right)^2-n^2\)

a)= \(\frac{\sqrt{2}-1}{2-1}+\frac{\sqrt{3}-\sqrt{2}}{3-2}+...+\frac{\sqrt{100}-\sqrt{99}}{100-99}\)
=\(\sqrt{2}-1+\sqrt{3}-\sqrt{2}+...+\sqrt{100}-\sqrt{99}\)
= \(-1+\sqrt{100}\)
= -1 +10
=9
b)Ta có\(\left(\sqrt{n+1}-\sqrt{n}\right)\cdot\left(\sqrt{n+1}+\sqrt{n}\right)\)=n+1-n=1 (1)
Lại có:\(\frac{1}{\sqrt{n+1}+1}\cdot\left(\sqrt{n+1}+1\right)=1\)(2)
Từ (1) và (2)=>\(\left(\sqrt{n+1}-1\right)=\frac{1}{\sqrt{n+1}+1}\)

Xét vế trái : \(\left(\sqrt{n+1}-\sqrt{n}\right)^2=2n+1-2\sqrt{n}.\sqrt{n+1}\)
Xét vế phải : \(\sqrt{\left(2n+1\right)^2}-\sqrt{\left(2n+1\right)^2-1}=\left|2n+1\right|-\sqrt{\left(2n+1-1\right)\left(2n+1+1\right)}\)
\(=2n+1-\sqrt{2n.2\left(n+1\right)}=2n+1-2\sqrt{n}.\sqrt{n+1}\)
=> VT = VP => đpcm