Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình hoành độ giao điểm của đồ thị (C) và trục Ox:
x3-3(m+1) x2+2(m2+4m+1)x-4m(m+1)=0
hay (x-2) (x2-(3m+1) x+2m2+2m)=0

Chọn A.

Loại bài này trước hết phải phân tích để mò coi pt có nghiệm cố định nào không:
\(x^3-3\left(m+1\right)x^2+2\left(m^2+4m+1\right)x-4m\left(m+1\right)=0\)
\(\Leftrightarrow2\left(x-2\right)m^2+\left(-3x^2+8x-4\right)m+\left(x^3-3x^2+2x\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}2\left(x-2\right)=0\\-3x^2+8x-4=0\\x^3-3x^2+2x=0\end{matrix}\right.\)
Cả 3 pt trên đều có nghiệm \(x=2\), vậy pt đã cho luôn có nghiệm cố định \(x=2\) với mọi m, sử dụng lược đồ Hoocne để hạ bậc ta đưa được pt về:
\(x^3-3\left(m+1\right)x^2+2\left(m^2+4m+1\right)x-4m\left(m+1\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2-\left(3m+1\right)x+2m^2+2m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x^2-\left(3m+1\right)x+2m^2+2m=0\left(1\right)\end{matrix}\right.\)
Để pt đã cho có 3 nghiệm pb đều lớn hơn 1 \(\Leftrightarrow\left(1\right)\) có 2 nghiệm pb lớn hơn 1 và khác 2
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\f\left(1\right)>0\\\frac{x_1+x_2}{2}>1\\f\left(2\right)\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\left(3m+1\right)^2-4\left(2m^2+2m\right)>0\\1-\left(3m+1\right)+2m^2+2m>0\\3m+1>2\\4-2\left(3m+1\right)+2m^2+2\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(m-1\right)^2>0\\2m^2-m>0\\m>\frac{1}{3}\\2m^2-4m+2\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m>\frac{1}{2}\\m\ne1\end{matrix}\right.\)

Đồ thị (C) cắt trục hoành tại điểm phân biệt tạo thành cấp số cộng khi và chỉ khi phương trình x3-3x2-1= m có ba nghiệm phân biệt lập thành cấp cố cộng.
Suy ra đường thẳng y=m đi qua điểm uốn của đồ thị y=x3-3x2-1 (do đồ thị (C) nhận điểm uốn làm tâm đối xứng).
Mà điểm uốn của y= x3-3x2-1 là I(1 ; -3) .
Suy ra m=-3.
Chọn C.

+ Đồ thị C cắt trục hoành tại điểm phân biệt tạo thành cấp số cộng khi và chỉ khi phương trình x3- 3x2- 1=m có ba nghiệm phân biệt lập thành cấp cố cộng.
+ Suy ra đường thẳng y= m đi qua điểm uốn của đồ thị y= x3- 3x2- 1
(do đồ thị (C) nhận điểm uốn làm tâm đối xứng).
+ Mà điểm uốn của đồ thị đã cho là I( 1 ; -3)
( hoành độ điểm uốn là nghiệm phương trình y’’= 0 hay y’’= 6x-6=0 do đó x= 1 ; y= -3)
Suy ra m= -3.
Chọn C.

Đáp án là A
Phương trình hoành độ giao điểm của đồ thị hàm số đã cho và trục hoành:
![]()
![]()
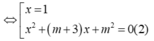
Đồ thị hàm số đã cho cắt trục hoành tại 3 điểm phân biệt ⇔ (1) có 3 nghiệm phân biệt ⇔ (2) có 2 nghiệm phân biệt khác 1
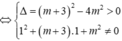
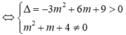
![]()
Do đó có 3 giá trị nguyên của m thỏa mãn ycbt.

+ Phương trình hoành độ giao điểm của (C) và đường thẳng d:
=x4- (2m-1) x2+2m = 2 hay x4- (2m-1) x2+2m -2=0
Suy ra x2= 1 hoặc x2= 2m-2 (1)
+ Đường thẳng d cắt C tại bốn điểm phân biệt có hoành độ nhỏ hơn 3 khi và chỉ khi phương trình (1) có hai nghiệm phân biệt nhỏ hơn 3.
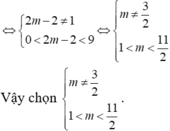
Do đó có 4 giá trị nguyên của m thỏa mãn đầu bài.
Chọn D.

Đáp án B
Phương pháp:
+) Xác định m để phương trình hoành độ giao điểm có 3 nghiệm phân biệt.
+) Cô lập m, sử dụng phương pháp hàm số.
Cách giải:
Phương trình hoành độ giao điểm của đồ thị hàm số y = x3 - mx + 1 và trục hoành là: x3 - mx + 1 = 0
⇔ x3 - mx + 1 = 0 ⇔ mx = x3 + 1(*)
+) x = 0:(*) ⇔ m.0 = 1: vô lý Phương trình (*) không có nghiệm x = 0 với mọi m
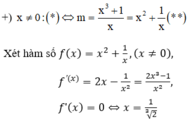
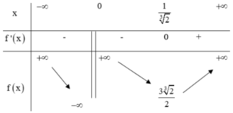
Số nghiệm của phương trình (**) là số giao điểm của đồ thị hàm số ![]() và đường thẳng y = m song song với trục hoành.
và đường thẳng y = m song song với trục hoành.
Để phương trình ban đầu có 3 nghiệm phân biệt ⇔ (**) có 3 nghiệm phân biệt khác 0

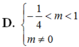

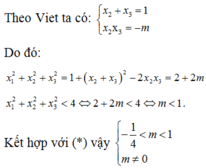



+ Phương trình hoành độ giao điểm của đồ thị C và trục Ox:
x3- 3( m+ 1) x2+ 2( m 2+ 4m+1 )= 0
hay ( x- 2) ( x2-( 3m+ 1) x+ 2m2+ 2m) =0
Yêu cầu bài toán
Vậy ½< m và m≠ 1.
Chọn A.