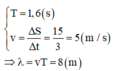Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dùng bút thử tiền chiếu vào một chỗ trên đường kẻ đó, nếu chỗ đó sáng lên ánh sáng màu vàng hay màu lục thì đó là chất phát quang.

Mình cũng không hiểu đề lắm :)
Mà các bài toán về va chạm không thi đâu bạn ơi, không nên học.
Không chắc lắm:
+) TH1 v1\(\uparrow\downarrow\)v2 => A=2cm ( vận tốc tại biên = 0)
+) TH2 v1\(\uparrow\uparrow v2\) => \(v=\frac{m1.v1+m2.v2}{m1+m2}=v1\Rightarrow\)cơ năng vật ( m1+m2) sau va chạm 1/2(m1+m2).V^2=1/2.k.A^2 suy ra A=2A0

Ta sử dụng quan hệ giữa chu kì và bước sóng:
\(\frac{t}{T}=\frac{s}{\lambda}\Rightarrow\lambda=9\left(m\right)\)
Mà : \(v=\frac{\lambda}{T}=5\) (cm/s)

Đáp án B
Ta có: Khoảng cách giữa hai vật nhỏ của con lắc bằng: ![]()
Ta có:
![]()
Biên độ tổng hợp của
x
1
-
x
2
là:![]()
![]()

a) Những đường kẻ này dùng để báo hiệu cho người đi đường nhìn thấy.
b) Các đường kẻ này làm bằng chất liệu phát quang.
c) Dùng bút thử tiền chiếu vào một chỗ trên đường kẻ đó, nếu chỗ đó sáng lên ánh sáng màu vàng hay màu lục thì đó là chất phát quang.

Đáp án C
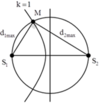
+ Điều kiện để một điểm M dao động cực đại và cùng pha với nguồn: d 2 - d 1 = k λ d 2 + d 1 = n λ
với k và n cùng chẵn hoặc cùng lẽ.
+ M gần trung trực nhất → k = 1 , để M nằm trong nửa đường tròn thì S 1 S 2 ≤ d 1 + d 2 ≤ d 1 m a x + d 2 m a x (1).
+ Với d 2 m a x - d 1 m a x = 4 d 2 m a x 2 + d 1 m a x 2 = 20 2 ⇒ d 1 m a x = 12 c m d 2 m a x = 16 c m
+ Thay vào (1), ta tìm được 5 ≤ n ≤ 7 , chọn 5, 7 (cùng lẻ vì k = 1), với n = 5 ứng với điểm nằm trên S 1 S 2 → trong đường tròn có 3 điểm cực đại, cùng pha với nguồn và nằm trên dãy k =1.

Chọn B
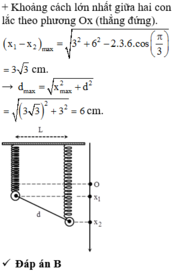
+ Khoảng cách giữa hai vật nhỏ trong quá trình dao động xác định theo công thức:
![]()
+ Đặt: X = x1 – x2 = 3cosωt - 6cos(ωt+π/3) = 3√3 sinωt
+ L có giá trị lớn nhất khi│X│ = Xmax = 3√3
=> Do vậy Lmax = 6cm.