\(=>8x+1\ge6x+2x\)

\(=>8x+1>8x\)

một đề bài lố bịch, một câu tl ngớ ngẩn, thế này mà olm có câu:

không có học trò dốt

mà chỉ có thầy chưa giỏi

em xin đổi lại là:

95% hs k biêt hoc toán

95% thầy cô trẻ dạy toán, rất giỏi toán

( vì điểm thi đh ở đhsp ngành toán lấy rất cao,em chỉ nói lên sự thật mong olm đừng trừ điểm)

\(=x^3\left(x+2\right)-x\left(x+2\right)\)

\(=\left(x+2\right)\cdot x\cdot\left(x+1\right)\left(x-1\right)\)

Vì đây là tích của bốn số nguyên liên tiếp

nên \(\left(x+2\right)\cdot x\cdot\left(x+1\right)\cdot\left(x-1\right)⋮24\)

Bài 4.

\(A=2x^3+(x+1)^3-3x(x-2)(x+2)-3(x^2+5x+9)\\=2x^3+(x^3+3x^2+3x+1)-3x(x^2-4)-3x^2-15x-27\\=2x^3+x^3+3x^2+3x+1-3x^3+12x-3x^2-15x-27\\=(2x^3+x^3-3x^3)+(3x^2-3x^2)+(3x+12x-15x)+(1-27)\\=-26\\---\)

\(B=x(x-4x)+x(2-x)(x+2)+4(2x^2-5x+4)\\=x\cdot(-3x)+x(2-x)(2+x)+8x^2-20x+16\\=-3x^2+x(4-x^2)+8x^2-20x+16\\=-3x^2+4x-x^3+8x^2-20x+16\)

Bạn kiểm tra lại đề giúp mình!

\(C=(x-2y)(x^2+2xy+4y^2)-(x^3-8y^3+10)\) (sửa đề)

\(=x^3-(2y)^3-x^3+8y^2-10\\=x^3-8y^3-x^3+8y^3-10\\=(x^3-x^3)+(-8y^3+8y^3)-10\\=-10\)

Bài 5.

\(d)xy^2-3x^3y^2-2x(xy-3xy^2)\\=xy^2-3x^3y^2-2x^2y+6x^2y^2\\---\\f)(x-y)(2x+y)-2x^2+y^2+3xy\\=x(2x+y)-y(2x+y)-2x^2+y^2+3xy\\=2x^2+xy-2xy-y^2-2x^2+y^2+3xy\\=(2x^2-2x^2)+(xy-2xy+3xy)+(-y^2+y^2)\\=2xy\)

\(Toru\)

cảm ơn bạn nhiều nhé. Câu C mình gõ phím vội nên quên mất ;để mik sửa

C=(x-2y)(x²+2xy+4x²)-(x³-8y³+10)

d: Ta có: \(\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)=24\)

\(\Leftrightarrow\left(x^2+5x+4\right)\left(x^2+5x+6\right)-24=0\)

\(\Leftrightarrow x\left(x+5\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)

1: \(=x^2+1\)

3: \(=\left(x-y-z\right)^2\)

a) Ta có: x4 - 1 = (x2 + 1)(x2-1), trong đó : x2 + 1 > 0, với mọi x.

Vậy điều kiện : x2 – 1 ≠ 0

x2 – 1 = (x – 1)(x + 1) ≠ 0 ⇒ x ≠ ±1

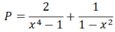
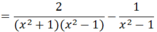
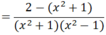
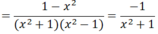
Do x2 + 1 > 0 với mọi x nên P < 0 với mọi x ≠ ±1

a) \(A=x^2-2x+2=\left(x-1\right)^2+1>0\forall x\inℝ\)

b) \(x-x^2-3=-\left(x^2-x+3\right)\)

\(=-\left(x^2-x+\frac{1}{4}+\frac{11}{4}\right)\)

\(=-\left[\left(x-\frac{1}{2}\right)^2+\frac{11}{4}\right]\)

\(=-\left[\left(x-\frac{1}{2}\right)^2\right]-\frac{11}{4}\le\frac{-11}{4}< 0\forall x\inℝ\)

x²-2x+2=(x²-2x+1)+1=( x-1)²+1

Mà (x-1)²≥0 với mọi x

=> (x-1)²+1>0 với mọi x

=> x²-2x+2>0 với mọi x

a: \(x^2-5x+10\)

\(=x^2-2\cdot x\cdot\dfrac{5}{2}+\dfrac{25}{4}+\dfrac{15}{4}\)

\(=\left(x-\dfrac{5}{2}\right)^2+\dfrac{15}{4}>0\forall x\)

b: \(2x^2+8x+15\)

\(=2\left(x^2+4x+\dfrac{15}{2}\right)\)

\(=2\left(x^2+4x+4+\dfrac{7}{2}\right)\)

\(=2\left(x+2\right)^2+7>0\forall x\)

Cảm ơn ạ