\(A=2x^3+6x^2-3x+\dfrac{1}{2}=2\cdot\dfrac{1}{3}^3+6\cdot\dfrac{1}{3}^2-3\cdot\dfrac{1}{3}+\dfrac{1}{2}\)

=13/54

Ta có: \(6x^2\ge0\)

\(2x< 6x^2\)

\(\Rightarrow6x^2+2x\ge0\)

\(\Rightarrow6x^2+2x+2017\ge2017\)

Vậy không tồn tại x khi đa thức trên bằng 0

Ta có hai trường hợp như sau :

TH1

\(x-2016\ge0\Leftrightarrow x\ge2016\) thì \(A=x-2016+x-1=2x-2017\ge2.2016-2017=2015\)

TH2

\(x-2016\le0\Leftrightarrow x\le2016\) thì \(A=2016-x+x-1=2015\)

vì vậy GTNN của A=2015

dấu bằng xảy ra khi \(x\le2016\)

C

C

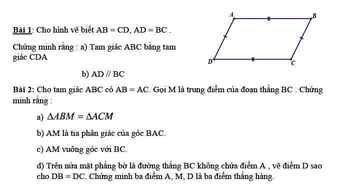
Bài 1:

a, Xét ΔABC và ΔCDA có:

AB=CD(gt)

AD=BC(gt)

Chung AC

⇒ΔABC = ΔCDA (c.c.c)

b, ΔABC = ΔCDA(cma) ⇒\(\widehat{ACB}=\widehat{CAD}\) ( 2 góc tương ứng)

Mà 2 góc này ở vị trị so le trong với nhau ⇒ AD // BC

Bn vẽ hình bài 1 cho mik đc ko ạ! Mik chưa hiểu rõ lắm!

(x^2+1)(x-1)(x+3)>0

Vì x^2+1>0 với mọi x

nên: (x-1)(x+3)>0

Trường hợp 1:

x-1<0, x+3 <0

Vì x+3 > x-1 nên x+3<0 suy ra x<-3

Trường hợp 2:

x-1>0, x+3>0

Vì x-1<x+3 nên x-1 >0 suy ra x>1

Vậy x<-3 hoặc x>1

Vì tích 3 số là số dương nên trong 3 số có thể gồm 2 số âm, 1 số dương hoặc cả 3 số đều dương

TH1: Có 2 số âm, 1 số dương

Trước hết ta có \(x+3>x-1\)

\(x^2+1>x-1\)

Vì vậy \(x-1< 0\)

\(x^2+1>0\) nên \(x+3< 0\)

\(\Rightarrow x< -3\left(< 1\right)\)

TH2: Cả 3 số đều dương

Xét số bé nhất lớn hơn 0:

\(x-1>0\Rightarrow x>1\)

Vậy \(\orbr{\begin{cases}x< -3\\x>1\end{cases}}\)

Câu 2: 

b: \(\Leftrightarrow2n-4+9⋮n-2\)

\(\Leftrightarrow n-2\in\left\{1;-1;3;-3;9;-9\right\}\)

hay \(n\in\left\{3;1;5;-1;11;-7\right\}\)

Câu 1: 

a: \(=\dfrac{3^{44}\cdot3^{17}}{3^{30}\cdot3^{13}}=3^{18}\)

b: \(=-2+\dfrac{1}{19-\dfrac{1}{2+1:\dfrac{3}{2}}}=-2+\dfrac{1}{19-\dfrac{3}{8}}\)

\(=-2+1:\dfrac{149}{8}=-2+\dfrac{8}{149}=-\dfrac{290}{149}\)