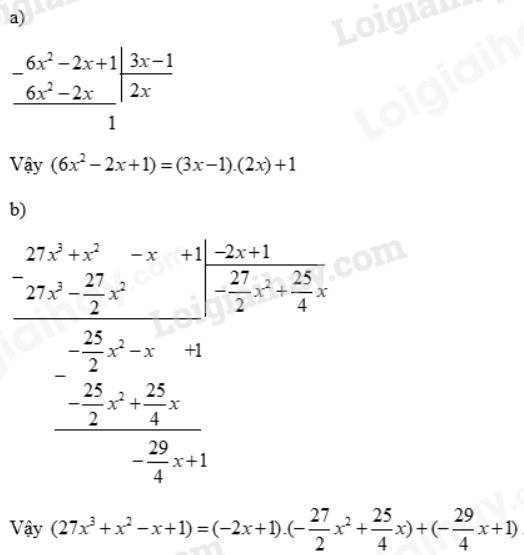a) \(({x^2} + 2x + 3) + (3{x^2} - 5x + 1) = ({x^2} + 3{x^2}) + (2x - 5x) + (3 + 1) = 4{x^2} - 3x + 4\);        

b) \(\begin{array}{l}(4{x^3} - 2{x^2} - 6) - ({x^3} - 7{x^2} + x - 5) = 4{x^3} - 2{x^2} - 6 - {x^3} + 7{x^2} - x + 5\\ = (4{x^3} - {x^3}) + ( - 2{x^2} + 7{x^2}) - x + ( - 6 + 5) = 3{x^3} + 5{x^2} - x - 1\end{array}\);

c) \(\begin{array}{l} - 3{x^2}(6{x^2} - 8x + 1) =  - 3{x^2}.6{x^2} -  - 3{x^2}.8x +  - 3{x^2}.1\\ =  - 18{x^{2 + 2}} + 24{x^{2 + 1}} - 3{x^2} =  - 18{x^4} + 24{x^3} - 3{x^2}\end{array}\);               

d) \(\begin{array}{l}(4{x^2} + 2x + 1)(2x - 1) = (4{x^2} + 2x + 1).2x - (4{x^2} + 2x + 1).1 = 4{x^2}.2x + 2x.2x + 1.2x - 4{x^2} - 2x - 1\\ = 8{x^{2 + 1}} + 4{x^{1 + 1}} + 2x - 4{x^2} - 2x - 1 = 8{x^3} + 4{x^2} + 2x - 4{x^2} - 2x - 1 = 8{x^3} - 1\end{array}\);

e) \(\begin{array}{l}({x^6} - 2{x^4} + {x^2}):( - 2{x^2}) = {x^6}:( - 2{x^2}) - 2{x^4}:( - 2{x^2}) + {x^2}:( - 2{x^2})\\ =  - \dfrac{1}{2}{x^{6 - 2}} + {x^{4 - 2}} - \dfrac{1}{2}{x^{2 - 2}} =  - \dfrac{1}{2}{x^4} + {x^2} - \dfrac{1}{2}.\end{array}\);  

g) 

 \(({x^5} - {x^4} - 2{x^3}):({x^2} + x)=x^3-2x^2\)

a: =>(3/2-2x):2/3=1/6

=>3/2-2x=1/6x2/3=2/18=1/9

=>2x=25/18

hay x=25/36

b: \(\Leftrightarrow2x-2x+\dfrac{5}{2}-2=x-\dfrac{1}{4}\)

=>x-1/4=1/2

=>x=3/4

c: \(\Leftrightarrow2x-\dfrac{2}{3}-\dfrac{1}{3}x+\dfrac{1}{4}x=0\)

=>23/12x=2/3

=>x=8/23

1) \(x^2\left(2x^3-x^2+4x\right)\)

\(=2x^5-x^4+4x^3\)

2) \(\left(x+2\right)\left(5x^3-3x^2+x\right)\)

\(=5x^4-3x^3+x^2+10x^3-6x^2+2x\)

\(=5x^4+7x^3-5x^2+2x\)

3) \(\left(x^2-2\right)\left(x^2+2x-1\right)\)

\(=x^4+2x^3-x^2-2x^2-4x+2\)

\(=x^4+2x^3-3x^2-4x+2\)

4) \(\left(x^2+x+1\right)\left(x-1\right)\)

\(=x^3-x^2+x^2-x+x-1\)

\(=x^3-1\)

Bạn nên viết lại đề bài cho sáng sủa, rõ ràng để người đọc dễ hiểu hơn.

f: =>4(x^2+4x-5)-x^2-7x-10=3(x^2+x-2)

=>4x^2+16x-20-x^2-7x-10-3x^2-3x+6=0

=>6x-24=0

=>x=4

e: =>8x+16-5x^2-10x+4(x^2-x-2)=4-x^2

=>-5x^2-2x+16+4x^2-4x-8=4-x^2

=>-6x+8=4

=>-6x=-4

=>x=2/3

d: =>2x^2+3x^2-3=5x^2+5x

=>5x=-3

=>x=-3/5

b: =>2x^2-8x+3x-12+x^2-7x+10=3x^2-12x-5x+20

=>-12x-2=-17x+20

=>5x=22

=>x=22/5

b: =>2x^2-8x+3x-12+x^2-7x+10=3x^2-17x+20

=>-12x-2=-17x+20

=>5x=22

=>x=22/5

c: =>24x^2+16x-9x-6-4x^2-16x-7x-28=20x^2-4x+5x-1

=>-16x-34=x-1

=>-17x=33

=>x=-33/17

d: =>2x^2+3x^2-3=5x^2+5x

=>5x=-3

=>x=-3/5

e: =>8x+16-5x^2-10x+4x^2-4x-8=4-x^2

=>-6x+8=4

=>-6x=-4

=>x=2/3

f: =>4(x^2+4x-5)-x^2-7x-10=3x^2+3x-6

=>4x^2+16x-20-4x^2-10x+4=0

=>6x=16

=>x=8/3

a) \(\frac{x}{x+1}=\frac{1}{2}\)

=> 2x = x + 1

=> 2x - x = 1

=> x = 1

b) \(\frac{x}{2}=\frac{x}{3}\)

=> 3x = 2x

=> 3x - 2x = 0

=> x = 0

c) \(\frac{x+1}{2}=\frac{x+1}{2017}\)

=> \(2017\left(x+1\right)=2\left(x+1\right)\)

=> 2017x + 2017 = 2x + 2

=> 2017x - 2x = 2 - 2017

=> 2015x = -2015

=> x = -2015 : 2015

=> x = -1

i) \(\frac{3}{x}=\frac{x}{2017}\)

=> x² = 2017.3

=> x² = 6051

=> \(\orbr{\begin{cases}x=\sqrt{6051}\\x=-\sqrt{6051}\end{cases}}\)

còn lại tự lm

\(a,\frac{x}{x+1}=\frac{1}{2}\)

\(\Rightarrow x=\frac{1}{2}.\left(x+1\right)\)

\(\Rightarrow x=\frac{1}{2}x+\frac{1}{2}\)

\(\Rightarrow x-\frac{1}{2}x=\frac{1}{2}\)

\(\Rightarrow\frac{1}{2}x=\frac{1}{2}\)

\(\Rightarrow x=1\)

\(b,\frac{x}{2}=\frac{x}{3}\)

\(\Rightarrow x=\frac{x}{3}.2\)

\(\Rightarrow x=\frac{2x}{3}\)

\(\Rightarrow3x=2x\)

\(\Rightarrow x=0\)

\(c,\frac{x+1}{2}=\frac{x+1}{2017}\)

\(\Rightarrow x+1=\frac{x+1}{2017}.2\)

\(\Rightarrow x+1=\frac{2x+2}{2017}\)

\(\Rightarrow2017x+2017=2x+2\)

\(\Rightarrow2017x-2x=2-2017\)

\(\Rightarrow2015x=-2015\)

\(\Rightarrow x=-1\)

\(i,\frac{3}{x}=\frac{x}{2017}\)

\(\Rightarrow x=3:\frac{x}{2017}\)

\(\Rightarrow x=\frac{6051}{x}\)

\(\Rightarrow x^2=6051\)

\(\Rightarrow x=\sqrt{6051}\)

\(o,\frac{x}{3}=\frac{x+1}{2}\)

\(\Rightarrow x=\frac{x+1}{2}.3\)

\(\Rightarrow x=\frac{3x+3}{2}\)

\(\Rightarrow2x=3x+3\)

\(\Rightarrow-x=3\)

\(\Rightarrow x=-3\)

\(m,\frac{x+1}{2}=\frac{x+2}{3}\)

\(\Rightarrow x+1=\frac{x+2}{3}.2\)

\(\Rightarrow x+1=\frac{2x+4}{3}\)

\(\Rightarrow3x+3=2x+4\)

\(\Rightarrow x=1\)

\(p,\frac{x+1}{2}=x\)

\(\Rightarrow2x=x+1\)

\(\Rightarrow x=1\)

\(m,\frac{2}{x}=\frac{x}{8}\)

\(\Rightarrow x=2:\frac{x}{8}\)

\(\Rightarrow x=\frac{16}{x}\)

\(\Rightarrow x^2=16\)

\(\Rightarrow x=4\)

\(Q,\frac{x^2}{2}=\frac{8}{x^2}\)

\(\Rightarrow x^2=\frac{8}{x^2}.2\)

\(\Rightarrow x^2=\frac{16}{x^2}\)

\(\Rightarrow x^4=16\)

\(\Rightarrow x=2\)

\(r,\frac{x^3}{2}=\frac{32}{x}\)

\(\Rightarrow x^3=\frac{32}{x}.2\)

\(\Rightarrow x^3=\frac{64}{x}\)

\(\Rightarrow x^4=64\)

\(\Rightarrow x=\sqrt[4]{64}\)

a: \(\dfrac{x-6}{7}+\dfrac{x-7}{8}+\dfrac{x-8}{9}=\dfrac{x-9}{10}+\dfrac{x-10}{11}+\dfrac{x-11}{12}\)

\(\Leftrightarrow\left(\dfrac{x-6}{7}+1\right)+\left(\dfrac{x-7}{8}+1\right)+\left(\dfrac{x-8}{9}+1\right)=\left(\dfrac{x-9}{10}+1\right)+\left(\dfrac{x-10}{11}+1\right)+\left(\dfrac{x-11}{12}+1\right)\)

=>x+1=0

hay x=-1

c: |x-2|=13

=>x-2=13 hoặc x-2=-13

=>x=15 hoặc x=-11

d: \(\Leftrightarrow3\left|x-2\right|+4\left|x-2\right|=2-\dfrac{1}{3}=\dfrac{5}{3}\)

=>7|x-2|=5/3

=>|x-2|=5/21

=>x-2=5/21 hoặc x-2=-5/21

=>x=47/21 hoặc x=37/21