Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cot a=1/5 nên cosa/sina=1/5
=>sina=5cosa
\(1+cot^2a=\dfrac{1}{sin^2a}=1+\dfrac{1}{25}=\dfrac{26}{25}\)
nên \(sina=\dfrac{5}{\sqrt{26}}\Leftrightarrow cosa=\dfrac{1}{\sqrt{26}}\)
\(cot^4a+sin^2a-cos^2a\)
\(=\dfrac{1}{5^4}+25cos^2a-cos^2a\)
\(=\dfrac{1}{5^4}+24\cdot\dfrac{1}{26}=\dfrac{7513}{8125}\)

\(1+cot^2a=\dfrac{1}{sin^2a}\)
\(\Leftrightarrow\dfrac{1}{sin^2a}=1+\dfrac{\left(a^2-b^2\right)^2}{4a^2b^2}=\dfrac{4a^2b^2+a^4-2a^2b^2+b^4}{4a^2b^2}\)
\(\Leftrightarrow sin^2a=\dfrac{4a^2b^2}{a^4+2a^2b^2+b^4}=\left(\dfrac{2ab}{\left(a^2+b^2\right)}\right)^2\)
=>\(cos^2a=\dfrac{a^4+2a^2b^2+b^4-4a^2b^2}{\left(a^2+b^2\right)^2}\)
\(\Leftrightarrow cos^2a=\dfrac{\left(a^2-b^2\right)^2}{\left(a^2+b^2\right)^2}\)
hay \(cosa=\dfrac{\left(a^2-b^2\right)}{a^2+b^2}\)

Bài 2:
\(\cos a=\sqrt{1-\left(\dfrac{7}{25}\right)^2}=\dfrac{24}{25}\)
\(\tan a=\dfrac{7}{25}:\dfrac{24}{25}=\dfrac{7}{24}\)
\(\cot a=\dfrac{24}{7}\)

Câu 1:
\(1+\cot^2a=\dfrac{1}{\sin^2a}\)
nên \(\dfrac{1}{\sin^2a}=1+5^2=26\)
\(\Leftrightarrow\sin^2a=\dfrac{1}{26}\)
\(\Leftrightarrow\sin a=\dfrac{\sqrt{26}}{26}\)
\(\cos a=\sqrt{1-\dfrac{1}{26}}=\dfrac{5\sqrt{26}}{26}\)
\(A=\dfrac{\sin a+\cos a}{\sin a-\cos a}=\left(\dfrac{\sqrt{26}+5\sqrt{26}}{26}\right):\left(\dfrac{\sqrt{26}-5\sqrt{26}}{26}\right)\)
\(=\dfrac{6\sqrt{26}}{-4\sqrt{26}}=\dfrac{-3}{2}\)

Đặt \(x=\alpha\)
a: \(\dfrac{1}{\cos^2x}=1+\tan^2x=1+\dfrac{1}{9}=\dfrac{10}{9}\)
nên \(\cos x=\dfrac{3\sqrt{10}}{10}\)
=>\(\sin x=\dfrac{\sqrt{10}}{10}\)
b: \(\dfrac{1}{\sin^2x}=1+\cot^2x=1+\dfrac{9}{16}=\dfrac{25}{16}\)
\(\Leftrightarrow\sin x=\dfrac{4}{5}\)
hay \(\cos x=\dfrac{3}{5}\)

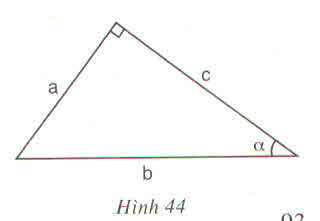
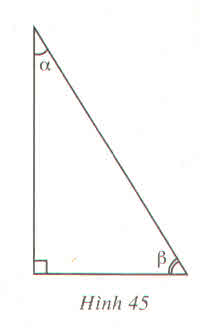
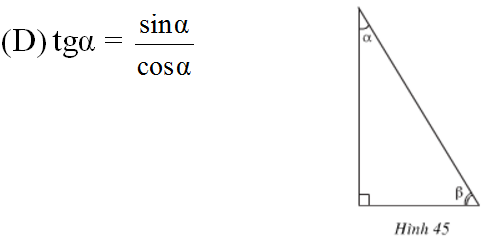
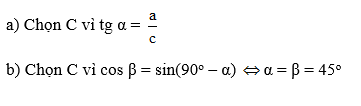

Chọn C