Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(f\left(-x\right)=\sqrt[3]{-x+2}-\sqrt[3]{-x-2}\)
\(=-\left(\sqrt[3]{x-2}-\sqrt[3]{x+2}\right)\)
=f(x)
Vậy: f(x) là hàm số chẵn

\(f\left(-x\right)=\left(-x\right)^{2020}-2\cdot\left(-x\right)^2-3\)
\(=x^{2020}-2x^2-3\)
=f(x)
=> f(x) là hàm số chẵn

Đáp án B
+ Hàm số f(x) và g(x) đều có tập xác định là D= R.
+ Xét hàm số y=f(x) : Với mọi ![]() và
và
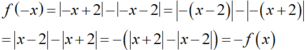
Nên y= f(x) là hàm số lẻ.
+ Xét hàm số y = g(x) :
Với mọi ![]() nên y = g(x) là hàm số chẵn.
nên y = g(x) là hàm số chẵn.
Chọn B.

TXĐ: D=R
\(y\left(-x\right)=\left(-x\right)^2+2=x^2+2=y\left(x\right)\)
\(\Rightarrow\) Hàm đã cho là hàm chẵn

\(TXD\) \(D=R\backslash\left\{0\right\}\) là tập đối xứng.
\(\forall x\in D\Rightarrow-x\in D\)
Có \(f\left(-x\right)=\dfrac{\left(-x\right)^2+1}{\left|2\left(-x\right)+1\right|+\left|2\left(-x\right)-1\right|}\)
\(=\dfrac{x^2+1}{\left|1-2x\right|+\left|-2x-1\right|}\)
\(=\dfrac{x^2+1}{\left|-\left(2x-1\right)\right|+\left|-\left(2x+1\right)\right|}\)
\(=\dfrac{x^2+1}{\left|2x-1\right|+\left|2x+1\right|}\) \(=f\left(x\right)\)
Vậy hàm số \(y=f\left(x\right)=\dfrac{x^2+1}{\left|2x+1\right|+\left|2x-1\right|}\) là hàm số chẵn.
TXĐ: D=R
Khi \(x\in D\) thì \(-x\in D\)
\(f\left(-x\right)=\dfrac{\left(-x\right)^2+1}{\left|-2x+1\right|+\left|-2x-1\right|}\)
\(=\dfrac{x^2+1}{\left|2x+1\right|+\left|2x-1\right|}=f\left(x\right)\)
=>f(x) chẵn

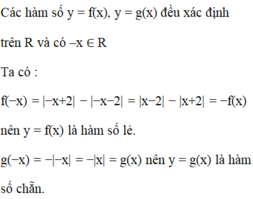
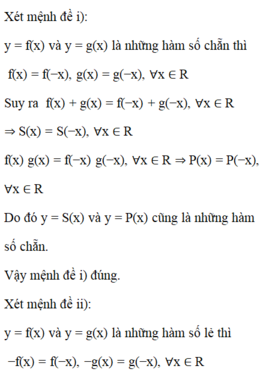
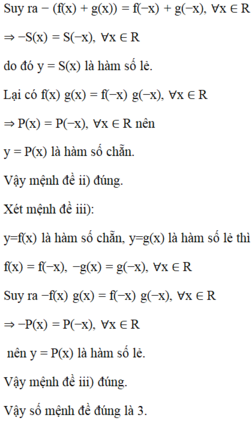
Đáp án A