
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\lim\limits_{x\rightarrow2}f\left(x\right)=\lim\limits_{x\rightarrow2}\dfrac{x^2+x-6}{x-2}=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(x+3\right)}{x-2}=\lim\limits_{x\rightarrow2}\left(x+3\right)=5\\ f\left(2\right)=5\\ \rightarrow\lim\limits_{x\rightarrow2}f\left(x\right)=f\left(2\right)\)
Suy ra f(x) liên tục tại x = 2.

a: \(\lim\limits_{x\rightarrow-2}f\left(x\right)=\lim\limits_{x\rightarrow-2}3x^2-2x+4\)
\(=3\cdot\left(-2\right)^2-2\cdot\left(-2\right)+4\)
\(=3\cdot4+4+4=20\)
\(f\left(-2\right)=3\cdot\left(-2\right)^2-2\left(-2\right)+4=20\)
=>\(\lim\limits_{x\rightarrow-2}f\left(x\right)=f\left(-2\right)\)
=>Hàm số liên tục tại x=-2
b: \(\lim\limits_{x\rightarrow3}f\left(x\right)=\lim\limits_{x\rightarrow3}2x^3-3x^2+1\)
\(=2\cdot3^3-3\cdot3^2+1\)
\(=2\cdot27-27+1=27+1=28\)
\(f\left(3\right)=2\cdot3^3-3\cdot3^2+1=54-27+1=28\)
=>\(\lim\limits_{x\rightarrow3}f\left(x\right)=f\left(3\right)\)
=>Hàm số liên tục tại x=3

\(TXD:ℝ\)
Ta xét: \(lim_{x\rightarrow3}\left(x^3+2x-1\right)=3^3+2.3-1=32\)
mà \(f\left(3\right)=32\)
=> \(lim_{x\rightarrow3}\left(x^3+2x-1\right)=f\left(3\right)\)
=> hàm số liên tục tại x=3

a) Ta có: g(2) = 5.
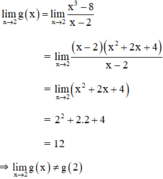
⇒ g(x) không liên tục tại x = 2.
b) Để g(x) liên tục tại x = 2
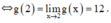
Vậy để hàm số liên tục tại x = 2 thì cần thay 5 bằng 12.

Lời giải:
\(\lim\limits_{x\to 1+}f(x)=\lim\limits_{x\to 1+}(5x-2)=3\)
\(\lim \limits_{x\to 1-}f(x)=\lim \limits_{x\to 1-}(2+2x)=4\)
\(\Rightarrow \lim\limits_{x\to 1+}f(x)\neq \lim \limits_{x\to 1-}f(x)\)
Do đó hàm số không liên tục tại $x=1$
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}2x+2=2\cdot1+2=4\)
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}5x-2=5-2=3\)
\(f\left(1\right)=2+2\cdot2=4\)
Vì \(\lim\limits_{x\rightarrow1^-}f\left(x\right)< >\lim\limits_{x\rightarrow1^+}f\left(x\right)\)
nên hàm số bị gián đoạn tại x=1

\(\lim\limits_{x\rightarrow1}f\left(x\right)=\lim\limits_{x\rightarrow1}\dfrac{2x^2-5x+3}{x-1}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(2x-3\right)}{x-1}=\lim\limits_{x\rightarrow1}2x-3=2\cdot1-3=-1\)
f(1)=4
=>\(\lim\limits_{x\rightarrow1}f\left(x\right)< >f\left(1\right)\)
=>Hàm số bị gián đoạn tại x=1
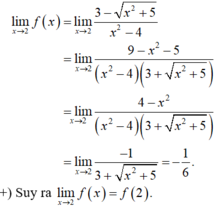
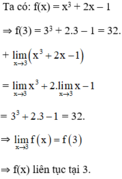
\(\lim\limits_{x\rightarrow3}f\left(x\right)=\lim\limits_{x\rightarrow3}-2x^2-4x=-2\cdot3^2-4\cdot3=-18-12=-30\)
\(f\left(3\right)=-2\cdot3^2-4\cdot3=-30\)
=>\(\lim\limits_{x\rightarrow3}f\left(x\right)=f\left(3\right)\)
=>f(x) liên tục tại x=3
Lời giải:
$\lim\limits_{x\to 3}f(x)=\lim\limits_{x\to 3}(-2x^2-4x)=-30=f(3)$ nên hàm liên tục tại $x=3$>