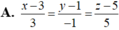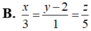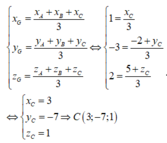Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A
Ta có:
AB² = 10, BC² = 24, AC² = 14 => ∆ABC vuông tại A.
Tâm I của đường tròn ngoại tiếp tam giác là trung điểm của BC => I (0;2;0).
Đường thẳng d cần tìm đi qua I (0;2;0) và nhận vectơ 
làm véc tơ chỉ phương. Phương trình chính tắc của đường thẳng d là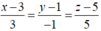 
\(\overrightarrow{AA'}=\left(0;0;3\right)=\overrightarrow{BB'}=\overrightarrow{CC'}\)
\(\Rightarrow\left\{{}\begin{matrix}B'\left(0;2;3\right)\\C'\left(-1;0;3\right)\end{matrix}\right.\)
\(\Rightarrow G\left(0;\dfrac{2}{3};3\right)\)
Đáp án A
Phương pháp giải: Xác định tọa độ ba điểm A, B, C và gọi tâm I, sử dụng điều kiện cách đều IA=IB=IC=IO để tìm tọa độ tâm I của mặt cầu
Lời giải:
Gọi A(a;0;0), B(0;b;0), C(0;0;c) => Tọa độ trọng tâm G là
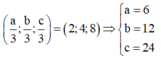
Gọi tâm mặt cầu (S) là I(x;y;z) => IO =IA = IB =IC
Vậy tọa độ tâm mặt cầu là I(3;6;12)
