Cho hình vẽ bên, biết PQ // AB, góc EAB = 70 độ; góc ANQ = 150 độ.
Tính số đo góc MEN.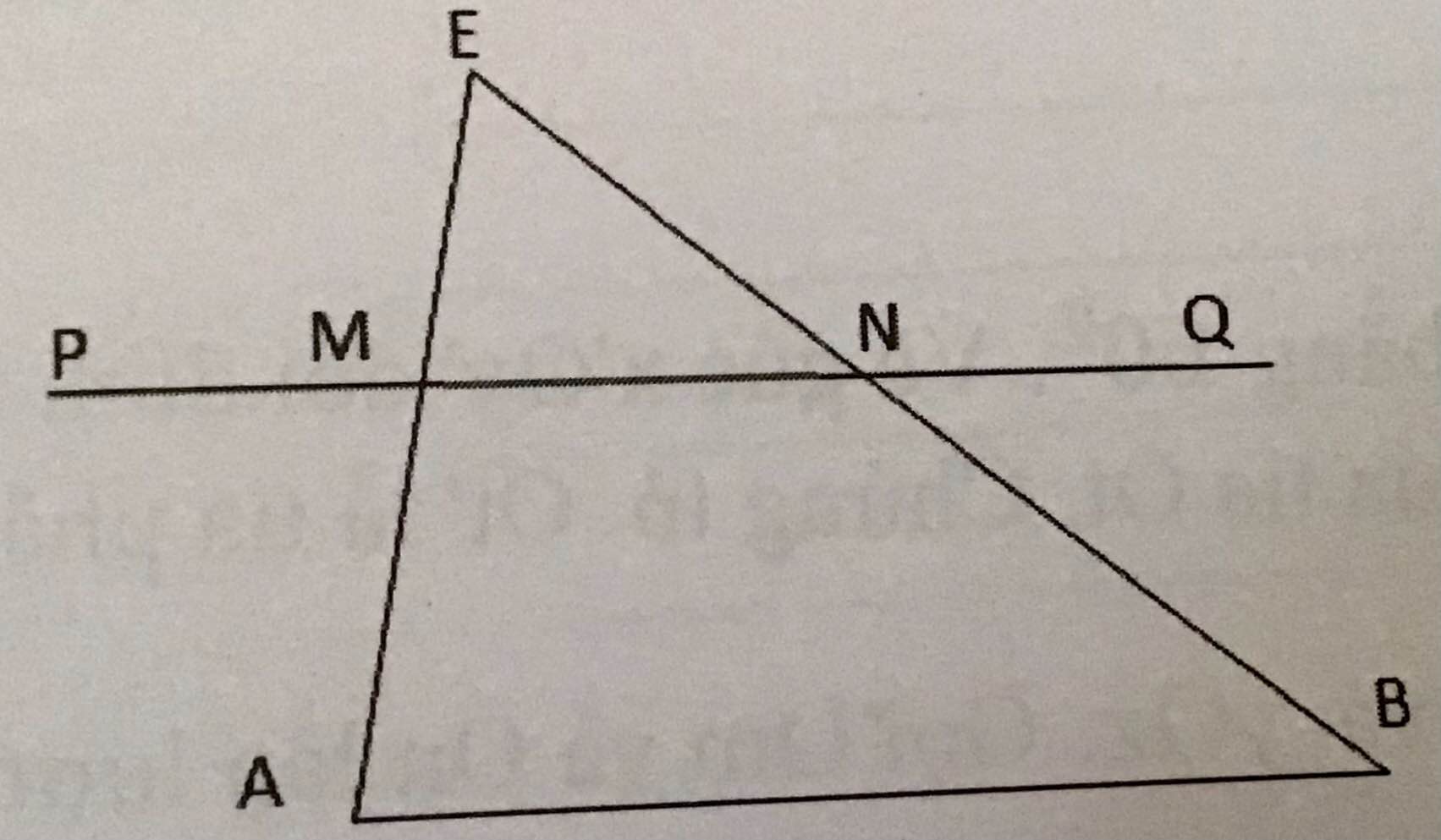
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TP
0
Những câu hỏi liên quan
EC
0
CM
28 tháng 10 2019
Ta có 50 × 50= 2500.
Vậy độ dài cạnh hình vuông ABCD là 50dm hay AB = BC = CD = AD = 50dm.
Ta có HBCD là hình thang vuông với chiều cao là cạnh BC, hai đáy là HB, DC.
Độ dài cạnh AH là:
50 : 100 × 70 = 35 (dm)
Độ dài cạnh HB là:
50 – 35 = 15 (dm)
Diện tích hình thang HBCD là:
(15 + 50) × 50 : 2 = 1625 ( d m 2 )
Đáp số: 1625 d m 2 .
Vậy đáp án đúng điền vào ô trống là 1625.
MQ
9 tháng 2 2023
Ta có 50 × 50= 2500.
Vậy độ dài cạnh hình vuông ABCD là 50dm hay AB = BC = CD = AD = 50dm.
Ta có HBCD là hình thang vuông với chiều cao là cạnh BC, hai đáy là HB, DC.
Độ dài cạnh AH là:
50 : 100 × 70 = 35 (dm)
Độ dài cạnh HB là:
50 – 35 = 15 (dm)
Diện tích hình thang HBCD là:
(15 + 50) × 50 : 2 = 1625 ( d m 2 )
Đáp số: 1625 d m 2 .
Vậy đáp án đúng điền vào ô trống là 1625.
DT
Đỗ Thanh Hải
CTVVIP
7 tháng 3 2021
Xét tam giác AEB và tam giác CED có
góc BAE = góc DCE = 90 độ
BE = CE
góc BEA = góc DEC (đối đỉnh)
=> tam giác AEB = tam giác CED (ch-gn)
b) Có tam giác AEB = tam giác CED => AB = CD
c) Xét tam giác ABC và tam giác CDA có
góc BAC = góc DCA = 90 độ
AB = CD
AC chung
=> tam giác ABC = tam giác CDA (c.g.c)
d) ta có tam giác ABC = tam giác CDA => góc BCA = góc DAC (2 góc tương ứng )
mà 2 góc ở vị trí so le trong => AD // BC
7 tháng 3 2021
a) Xét ΔEAB vuông tại A và ΔECD vuông tại C có
EB=ED(gt)
\(\widehat{AEB}=\widehat{CED}\)(hai góc đối đỉnh)
Do đó: ΔEAB=ΔECD(cạnh huyền-góc nhọn)
HC
9 tháng 10 2021
Do góc A1= góc D mà hai góc này là cặp góc đồng vị
-> AB // CD
Ta có góc ABC là góc đối đỉnh của góc B1 nên:
-> góc B1= góc ABC -> góc ABC = 115 độ
Do AB // CD nên tổng hai góc trong cùng phía bằng 180 độ
-> góc ABC + góc C = 180 độ -> góc C = 180 độ - 115 độ = 65 độ
8 tháng 10 2021
Ta có: \(\widehat{ABC}=\widehat{B_1}=115^0\)(đối đỉnh)
Ta có: \(\widehat{A_1}=\widehat{D}=70^0\)
Mà 2 góc này so le trong
=> AB//CD
\(\Rightarrow\widehat{ABC}+\widehat{C}=180^0\)(trong cùng phía)
\(\Rightarrow\widehat{C}=180^0-115^0=65^0\)
8 tháng 10 2021
Do góc A1= góc D mà hai góc này là cặp góc đồng vị
-> AB // CD
Ta có góc ABC là góc đối đỉnh của góc B1 nên:
-> góc B1= góc ABC -> góc ABC = 115 độ
Do AB // CD nên tổng hai góc trong cùng phía bằng 180 độ
-> góc ABC + góc C = 180 độ -> góc C = 180 độ - 115 độ = 65 độ