hinh thang chu

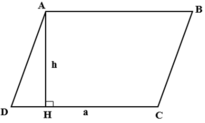
Ta có : S = a.h

Khi đó ta có: S = 4.2 = 8 c m 2 .

Chọn đáp án B.

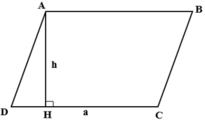
Ta có : S = a.h

Khi đó ta có: S = 4.2 = 8  c m 2 .

Chọn đáp án B. 

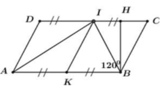
Kẻ BH là đường cao ứng với cạnh CD của hình bình hành ABCD

=> S_ABCD = BH.CD

Theo đề bài ta có chu vi hình bình hành ABCD bằng 60cm.

=> 2(AB + BC) = 60 ó 2.3BC = 60 ó BC = 10cm

Xét tứ giác KICB ta có:

IC = BC = KB = IK = 1 2 AB = 10cm

=> IKBC là hình thoi (dấu hiệu nhận biết).

Mà B ^ = 120⁰ =>  I C B ^  = 180⁰ – 120⁰ = 60⁰

Xét tam giác ICB có: I C = B C I C B = 60 0

=> ICB là tam giác đều. (tam giác cân có góc ở đỉnh bằng 60⁰).

=> BH vừa là đường cao vừa là đường trung tuyến ứng hay H là trung điểm của IC.

=> HI = HC = 1 2 BC = 5cm

Áp dụng định lý Pytago với tam giác vuông HBC ta có:

BH = B C 2 − H C 2 = 10 2 − 5 2 = 75 = 5 3 cm

=> S_ABCD = BH.AB = BH.2BC = 5 3 .2.10 = 100 3 cm²

Đáp án cần chọn là: A

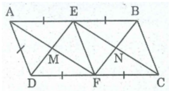
Ta có: Hình chữ nhật EMFN là hình thoi ⇒ ME = MF

ME = 1/2 DE (tính chất hình thoi)

MF = 1/2 AF (tính chất hình thoi)

Suy ra: DE = AF

⇒ Tứ giác AEFD là hình vuông (vì hình thoi có 2 đường chéo bằng nhau)

⇒ ∠ A = 90 0  ⇒ Hình bình hành ABCD là hình chữ nhật.

Ngược lại: ABCD là hình chữ nhật ⇒  ∠ A =  90 0

Hình thoi AEFD có ∠ A =  90 0  nên AEFD là hình vuông

⇒ AF = DE ⇒ ME = MF (tính chất hình vuông)

Hình chữ nhật EMFN là hình vuông (vì có 2 cạnh kề bằng nhau)

Vậy hình chữ nhật EMFN là hình vuông nếu ABCD là hình chữ nhật có AB = 2AD.

Giải cho m bài này 

Theo tích chất hình bình hành thì suy ra AB= DC= 15cm.

Chiều cao AH: 15 x \(\frac{3}{5}\)= 9 (cm)

Diện tính hình bình hành ABCD: 9 x 15 = 135 \(\left(cm^2\right)\)

Đáp số: 135 \(cm^2\)