câu 2 : Cho hình thang cân MNPQ có MN//PQ và MN<PQ. đường chéo NQ vuông góc vs cạnh bên NP, vẽ đường cao NH:
a) Chứng minh tam giác NPQ khác vs tam giác HPN.
b) Cho NP=15cm ; QP = 25cm . tính Hp,HQ. giúp em vs ak
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TV
1
TH
1
CM
5 tháng 10 2017
Đáp án cần chọn là: C
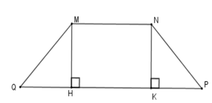
Kẻ MH ⊥ QP; NK ⊥ QP tại H, K => MH // NK
Tứ giác MNHK có MN // HK nên MNHK là hình thang, lại có MH // NK
=> MN = HK; MH = NK
(Vì hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau)
Lại có
MQ = NP (vì MNPQ là hình thang cân) suy ra ΔMQH = ΔNKP (ch – cgv)
=> QH = KP = Q P − H K 2
Mà HK = MN = 12 cm nên QH = KP = 40 − 12 2 = 14 cm
Mà M Q P ^ = 45 ° => ΔMHQ vuông cân tại H => MH = QH = 14 cm
Diện tích hình thang cân MNPQ là
SMNPQ = ( M N + P Q ) . M H 2 = ( 12 + 40 ) .14 2 = 364 c m 2
CM
21 tháng 2 2018
Đáp án cần chọn là: B
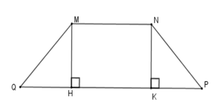
Kẻ MH ⊥ QP; NK ⊥ QP tại H, K => MH // NK
Tứ giác MNHK có MN // HK nên MNHK là hình thang, lại có MH // NK
=> MN = HK; MH = NK
(Vì hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau)
Lại có
MQ = NP (vì MNPQ là hình thang cân) suy ra ΔMQH = ΔNKP (ch – cgv)
=> QH = KP = Q P − H K 2
Mà HK = MN = 8 cm nên QH = KP = 30 − 8 2 = 8 cm
Mà M Q P ^ = 45 ° => ΔMHQ vuông cân tại H => MH = QH = 14 cm
Diện tích hình thang cân MNPQ là
SMNPQ = ( M N + P Q ) . M H 2 = ( 8 + 30 ) .11 2 = 209 c m 2 .
2N
1
29 tháng 1
ΔNIQ vuông tại I
=>\(NI^2+IQ^2=NQ^2\)
=>\(NQ^2=12^2+16^2=400\)
=>\(NQ=\sqrt{400}=20\)
Ta có: MNPQ là hình thang cân
=>MQ=NP
mà NP=15
nên MQ=15
Ta có: QP=QI+IP
=16+9
=25
Kẻ MK\(\perp\)PQ tại K
Xét ΔMKQ vuông tại K và ΔNIP vuông tại I có
MQ=NP
\(\widehat{MQK}=\widehat{NPI}\)
Do đó: ΔMKQ=ΔNIP
=>QK=IP=9cm
Ta có: QK+KI=QI
=>KI+9=16
=>KI=7(cm)
Xét tứ giác MNIK có
MN//IK
MK//IN
Do đó: MNIK là hình bình hành
=>MN=KI
mà KI=7cm
nên MN=7cm
12 tháng 8 2021
a: Hình thang MNPQ có MP=NQ
nên MNPQ là hình thang cân
b: Xét tứ giác MNKP có
MN//KP
MP//KN
Do đó: MNKP là hình bình hành
Suy ra: MP=NK
mà MP=NQ
nên NK=NQ
hay ΔNKQ cân tại N
3 tháng 8 2023
a: Xét tứ giác MNKP có
MN//KP
MP//NK
=>MNKP là hình bình hành
=>MP=NK
mà MP=NQ
nên NK=NQ
=>ΔNKQ cân tại N
b: MNKP là hbh
=>góc K=góc NMP
=>góc K=góc MPQ
=>góc MPQ=góc NQP
Xét ΔMQP và ΔNPQ có
MP=NQ
góc MPQ=góc NQP
QP chung
=>ΔMQP=ΔNPQ
c: ΔMQP=ΔNPQ
=>góc MQP=góc NPQ
=>MNPQ là hình thang cân
a)xét tam giác NPQ và tam giác HPN có:
góc PNQ=góc HPN =90 độ
góc P chung
\(\Rightarrow\Delta NPQ\infty\Delta HPN\left(g.g\right)\)
b) theo câu a) \(\Delta NPQ\infty\Delta HPN\) nên:
\(\dfrac{NP}{HP}=\dfrac{PQ}{PN}hay\dfrac{15}{HP}=\dfrac{25}{15}\Rightarrow HP=\dfrac{15\cdot15}{25}=\dfrac{225}{25}=9\left(cm\right)\)
HQ=PQ-HP=25-9=16(cm)