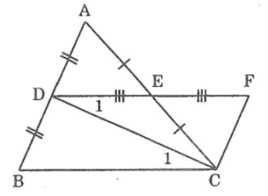
Cho tam giác ABC, gọi D, E lần lượt là trung điểm của của AB, AC, lấy F sao cho E là trung điểm của DF. Chứng minh rằng:
a) DB = CF; b) tam giác FCD=tam giác BDC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,\left\{{}\begin{matrix}AE=EC\\DE=EF\\\widehat{AED}=\widehat{CEF}\left(đđ\right)\end{matrix}\right.\Rightarrow\Delta ADE=\Delta CFE\left(c.g.c\right)\\ b,\Delta ADE=\Delta CFE\\ \Rightarrow AD=CF\\ \text{Mà }AD=DB\Rightarrow BD=CF\\ c,\Delta ADE=\Delta CFE\Rightarrow\widehat{ADE}=\widehat{CFE}\\ \text{Mà 2 góc này ở vị trí slt }\Rightarrow AB\text{//}CF\)
c: Xét tứ giác ADCF có
E là trung điểm của AC
E là trung điểm của DF
Do đó: ADCF là hình bình hành
Suy ra: AD//CF
hay AB//CF

Xét ΔADE và ΔCFE, ta có:
AE = CE ( Do E là trung điểm của AC).
∠(AED) =∠(CEF) (đối đỉnh)
DE = FE ( giả thiết)
Suy ra: ΔADE= ΔCFE (c.g.c)
⇒AD = CF (hai cạnh tương ứng)
Mà AD = DB ( vì D là trung điểm AB).
Vậy: DB = CF

a) xét tam giác ADE và tam giác FEC, ta có:
+) AE = EC (E là trung điểm của AC)
+) DE = EF (E là trung điểm của DF)
\(\widehat{ADE}=\widehat{CEF}\)(hai góc đối đỉnh)
=> \(\Delta ADE=\Delta FEC\) (c = g = c)
=> AD = CF (2 cạnh tương ứng)
mà AD = DB (D là trung điểm của AB)
nên: CF = BD
b) ta có:
\(\widehat{EAD}=\widehat{ECF}\left(\Delta ADE=\Delta FEC\right)\)
mà góc EAD và góc ECF nằm so le
nên AD//CF hay AB//CF
xét tam giác BDC và tam giác DCF, ta có:
BD = CF (Cm a)
DC = DC
\(\widehat{BDC}=\widehat{FCD}\)(2 góc so le trong và AB//CF)
=> \(\Delta BDC=\Delta DCF\)(c = g = c)
c) ta có:
\(DE=\frac{1}{2}DF\)(E là trung điểm DF)
DF = BC \(\left(\Delta FCD=\Delta BDC\right)\)
=> \(DE=\frac{1}{2}BC\)

b: Xét tứ giác ADCF có
E là trung điểm của AC
E là trung điểm của DF
Do đó: ADCF là hình bình hành
Suy ra: FC=AD
hay FC=DB
c: Ta có: ADCF là hình bình hành
nên CF//AD
hay CF//AB

a: Xét ΔAEC và ΔBEF có
EA=EB
\(\widehat{AEC}=\widehat{BEF}\)
EC=EF
Do đó: ΔAEC=ΔBEF
b) Ta có: △ AEC và △ BEF ( chứng minh trên )
Mà lại có: \(\widehat{ACE}=\widehat{BFE}\) ( 2 góc tương ứng )
Ta lại thấy hai góc này ở vị trí so le trong
Suy ra: AC // BF
a: Xét tứ giác BDFC có
FD//BC
FD=BC
Do đó: BDFC là hình bình hành
Suy ra: DB=FC