Cm rằng phương trình 2x2 - (m+4)x + m = 0 luôn có nghiệm
Ai biết làm giải dùm mình với đc ko ạ ~~
Mình cảm ơn nhìu <3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 10 2023
\(x^3-3x+2-2m=0\)
=>\(2m=x^3-3x+2\)
Chúng ta sẽ vẽ đồ thị \(y=x^3-3x+2\)
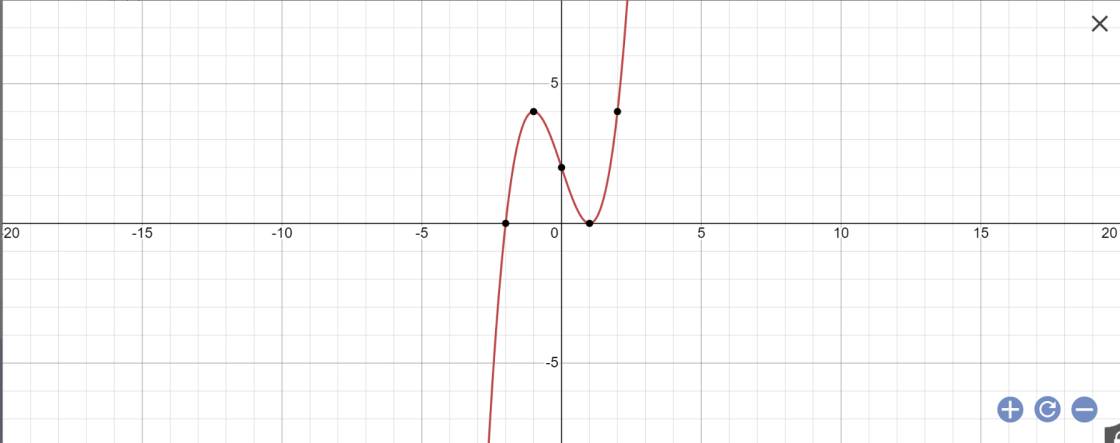
Trên đồ thị, chúng ta sẽ thấy khi \(y\in\left(0;4\right)\) thì \(y=x^3-3x+2\) sẽ cho 3 nghiệm phân biệt
=>\(2m\in\left(0;4\right)\)
=>\(m\in\left(0;2\right)\)
=>Chọn B
M
16 tháng 3 2022
-2\(x^2+xy^2\) (\(xy^2\) là \(1xy^2\) )
=(\(-2+1\)) (\(x^2.x\)) . \(y^2\) (Ta nhân số theo số và phần biến theo phần biến)
= -1\(x^3y^2\)
Tại \(x\)= -1 ; \(y\) = - 4 ta có
-1.(-1)\(^3\).(-4)\(^2\)= -1.(-1). 16 = 16
Vậy tại x= -1 ; y = - 4 biểu thức -2\(x^2+xy^2\) là 16
\(-x^2y+2y^2\) (\(-x^2y\) là \(-1x^2y\))
= (-1+2). \(x^2.\left(y.y^2\right)\)
= 1\(x^2y^3\)
Tại x= 0 ; y = - 2 ta có
1.\(\left(0\right)^2.\left(-2\right)^3\)= 1. 0. -8 = 0 (0 nhân với số nào cũng bằng 0)
Vậy tại x= 0 ; y = - 2 biểu thức \(-x^2y+2y^2\) là 0
NHỮNG CHỖ NÀO CÓ IN ĐẬM VÀ NGHIÊNG LÀ KHÔNG GHI NHA
15 tháng 5 2023
Thay x=7+căn 2022 vào pt, ta được:
\(49+14\sqrt{2022}+2022-7-\sqrt{2022}+3m-2=0\)
=>\(3m+2062+13\sqrt{2022}=0\)
=.\(m=\dfrac{-2062-13\sqrt{2022}}{3}\)
2x2 - ( m + 4 )x + m = 0
Δ = b2 - 4ac = ( m + 4 )2 - 8m = m2 + 8m + 16 - 8m = m2 + 16
Vì m2 + 16 ≥ 16 > 0 ∀ m => Δ ≥ 16 > 0
Vậy phương trình luôn có nghiệm ( đpcm )