Chứng minh :\(\left(\sqrt[3]{3+2.\sqrt{2}}+\sqrt[3]{3-2.\sqrt{2}}\right)^8>3^6\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(4-\sqrt{7}\right)^2=4^2-2\cdot4\cdot\sqrt{7}+7\)
\(=16-8\sqrt{7}+7=23-8\sqrt{7}\)
\(\sqrt{9-4\sqrt{5}}-\sqrt{5}\)
\(=\sqrt{5-2\cdot\sqrt{5}\cdot2+4}-\sqrt{5}\)
\(=\sqrt{\left(\sqrt{5}-2\right)^2}-\sqrt{5}\)
\(=\left|\sqrt{5}-2\right|-\sqrt{5}\)
\(=\sqrt{5}-2-\sqrt{5}=-2\)
\(\dfrac{\sqrt{4-2\sqrt{3}}}{1+\sqrt{2}}:\dfrac{\sqrt{2}-1}{\sqrt{3}+1}\)
\(=\dfrac{\sqrt{3-2\cdot\sqrt{3}\cdot1+1}}{\sqrt{2}+1}\cdot\dfrac{\sqrt{3}+1}{\sqrt{2}-1}\)
\(=\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{\sqrt{2}+1}\cdot\dfrac{\sqrt{3}+1}{\sqrt{2}-1}\)
\(=\dfrac{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}=\dfrac{3-1}{2-1}=2\)
\(\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}-\dfrac{6\sqrt{6}}{3}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{1}{2}\sqrt{6}-2\sqrt{6}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\dfrac{1}{2}-2=-\dfrac{3}{2}=-1,5\)

+) \(\left(\sqrt{4}-\sqrt{3}\right)^2=4-2\sqrt{4\cdot3}+3=7-2\sqrt{7}=\sqrt{49}-\sqrt{48}\)
+) \(2\sqrt{2}\left(2-3\sqrt{3}\right)+\left(1-2\sqrt{2}\right)^2+6\sqrt{6}\)
\(=4\sqrt{2}-6\sqrt{6}+9-4\sqrt{2}+6\sqrt{6}\)
\(=9\)
+) Sửa : \(\sqrt{8-2\sqrt{15}}-\sqrt{8+2\sqrt{15}}\)
\(=\sqrt{5-2\sqrt{5}\cdot\sqrt{3}+3}-\sqrt{5+2\sqrt{5}\cdot\sqrt{3}+3}\)
\(=\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}-\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}\)
\(=\sqrt{5}-\sqrt{3}-\sqrt{5}-\sqrt{3}\)
\(=-2\sqrt{3}\)



Đặt $x=\sqrt[3]{3+2\sqrt{2}},y=\sqrt[3]{3-2\sqrt{2}}$
$\Rightarrow \left\{\begin{matrix} x^{3}+y^{3}=6\\xy=1 \end{matrix}\right.$
$\Rightarrow (x+y)^{3}=x^{3}+y^{3}+3xy(x+y)=6+3xy=3[1+1+(x+y)]> 3.3\sqrt[3]{1.1.(x+y)}$
(Vì x>1,y>0=>x+y>1)
Do đó: $(x+y)^{3}> 3^{2}.\sqrt[3]{x+y}$
$\Rightarrow (x+y)^{9}>3^{6}.(x+y)$
$\Rightarrow (x+y)^{8}>3^{6}$
=>đpcm
Đặt $x=\sqrt[3]{3+2\sqrt{2}},y=\sqrt[3]{3-2\sqrt{2}}$
$\Rightarrow \left\{\begin{matrix} x^{3}+y^{3}=6\\xy=1 \end{matrix}\right.$
$\Rightarrow (x+y)^{3}=x^{3}+y^{3}+3xy(x+y)=6+3xy=3[1+1+(x+y)]> 3.3\sqrt[3]{1.1.(x+y)}$
(Vì x>1,y>0=>x+y>1)
Do đó: $(x+y)^{3}> 3^{2}.\sqrt[3]{x+y}$
$\Rightarrow (x+y)^{9}>3^{6}.(x+y)$
$\Rightarrow (x+y)^{8}>3^{6}$
=>đpcm


a) \(A=\frac{2+\sqrt{3}}{\sqrt{2}+\sqrt{2+\sqrt{3}}}+\frac{2-\sqrt{3}}{\sqrt{2}-\sqrt{2-\sqrt{3}}}=\sqrt{2}\)
Biến đổi vế trái :
VT = \(\frac{2+\sqrt{3}}{\sqrt{2}+\sqrt{2+\sqrt{3}}}+\frac{2-\sqrt{3}}{\sqrt{2}-\sqrt{2-\sqrt{3}}}\)
\(=\frac{\sqrt{2}\left(2+\sqrt{3}\right)}{\sqrt{2}\left(\sqrt{2}+\sqrt{2+\sqrt{3}}\right)}+\frac{\sqrt{2}\left(2-\sqrt{3}\right)}{\sqrt{2}\left(\sqrt{2}-\sqrt{2-\sqrt{3}}\right)}\)
\(=\frac{\sqrt{2}\left(2+\sqrt{3}\right)}{2+\sqrt{4+2\sqrt{3}}}+\frac{\sqrt{2}\left(2-\sqrt{3}\right)}{2-\sqrt{4-2\sqrt{3}}}=\frac{\sqrt{2}\left(2+\sqrt{3}\right)}{2+\left|\sqrt{3}+1\right|}+\frac{\sqrt{2}\left(2-\sqrt{3}\right)}{2-\left|\sqrt{3}-1\right|}\)
\(=\frac{\sqrt{2}\left(2+\sqrt{3}\right)}{2+\sqrt{3}+1}+\frac{\sqrt{2}\left(2-\sqrt{3}\right)}{2-\sqrt{3}+1}=\frac{\sqrt{2}\left(2+\sqrt{3}\right)}{\sqrt{3}+3}+\frac{\sqrt{2}\left(2-\sqrt{3}\right)}{3-\sqrt{3}}=\frac{\sqrt{2}\left(2+\sqrt{3}\right)\left(\sqrt{3}-3\right)+\sqrt{2}\left(2-\sqrt{3}\right)\left(\sqrt{3}+3\right)}{\left(\sqrt{3}+3\right)\left(3-\sqrt{3}\right)}\)
\(=\frac{\sqrt{2}\left(6-2\sqrt{3}+3\sqrt{3}-3+6+2\sqrt{3}-3\sqrt{3}-3\right)}{9-3}=\frac{6\sqrt{2}}{6}=\sqrt{2}=VP\left(đpcm\right)\)
b) \(B=\left(5+\sqrt{21}\right)\left(\sqrt{14}-\sqrt{6}\right)\sqrt{5-\sqrt{21}}=8\)
Biến đổi vế trái :
VT = \(\left(5+\sqrt{21}\right)\left(\sqrt{14}-\sqrt{6}\right)\sqrt{5-\sqrt{21}}=\sqrt{5+\sqrt{21}}\left(\sqrt{14}-\sqrt{6}\right)\sqrt{5+\sqrt{21}}\sqrt{5-\sqrt{21}}\)
\(=\sqrt{2}\sqrt{5+\sqrt{21}}\left(\sqrt{7}-\sqrt{3}\right)\sqrt{25-21}=\sqrt{10+2\sqrt{21}}\left(\sqrt{7}-\sqrt{3}\right)\sqrt{4}=\left|\sqrt{7}+\sqrt{3}\right|\left(\sqrt{7}-\sqrt{3}\right)2\)
\(=\left(\sqrt{7}+\sqrt{3}\right)\left(\sqrt{7}-\sqrt{3}\right)2=\left(7-3\right)2=4.2=8=VP\left(đpcm\right)\)

`e)(3/2sqrt6+2sqrt{2/3}-4sqrt{3/2})(3/2sqrt6+2sqrt{2/3}+4sqrt{3/2})`
`=(3/2sqrt6+2sqrt{2/3})^2-(4\sqrt{3/2})^2`
`=((3sqrt6)/2+(2sqrt2)/3)^2-16*3/2`
`=((9sqrt6)/6+(4sqrt6)/6)^2-24`
`=((13sqrt6)/6)^2-24`
`=13^2/6-24`
`=25/6`
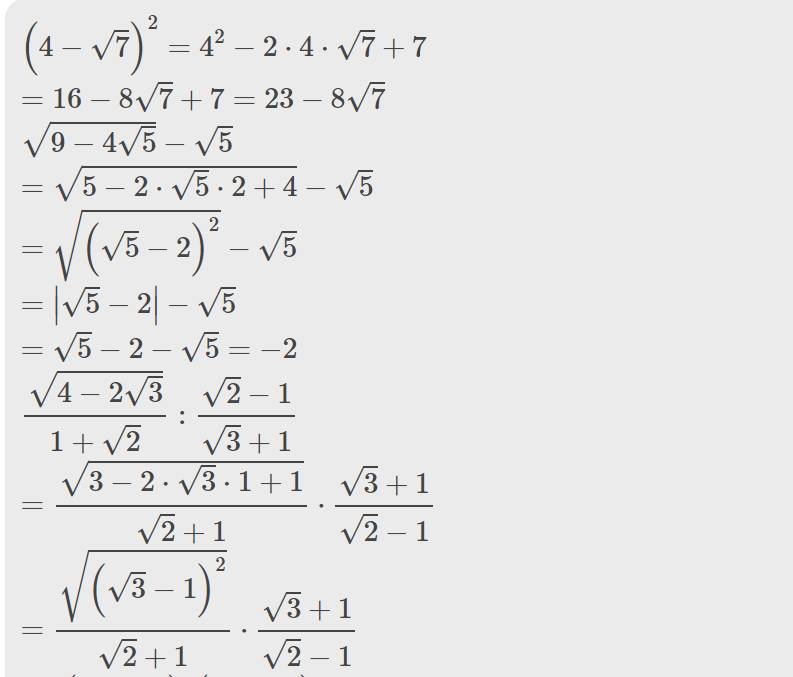
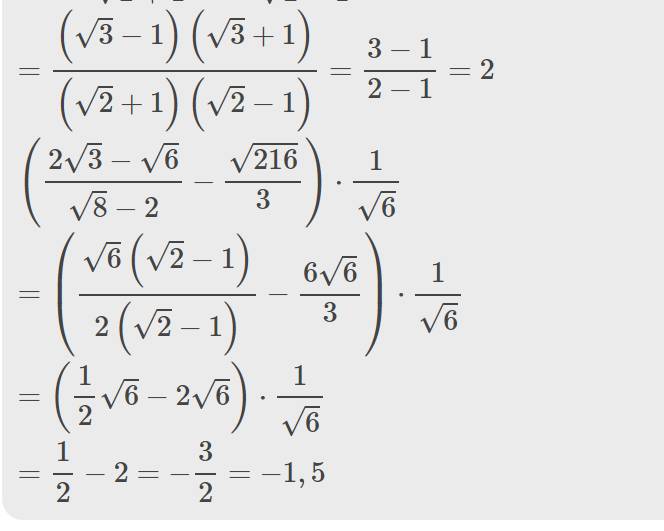
HFGBHGHFGHFGFGHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHHGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGGG