Tính giá trị của biểu thức sau tại x = 1 và y = -1:
\(\frac{1}{2}\) x5y - \(\frac{3}{4}\) x5y + x5y.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


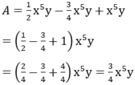
Thay x = 1 và y = - 1 vào biểu thức A sau khi rút gọn ta có:
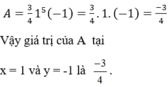

\(=-\left(-1\right)^5\cdot1+\left(-1\right)^2\cdot1+\left(-1\right)^5\cdot1=1+1-1=1\)


1.
\(\frac{-2}{3}x^3y^4.\left(\frac{-5}{9}x^5y\right).3y^7=\left[\left(\frac{-2}{3}\right).\left(\frac{-5}{9}\right).3\right]\left(x^3y^4x^5yy^7\right)=\frac{10}{9}x^8y^{12}\ge0\)
Vậy 3 đơn thuc trên không thể có cùng gt âm (vì nếu cùng âm thì tích của chúng phải âm)

Để x5y chia hết cho 2 và 5 thì y = 0
Để x50 chia hết cho 3 thì x = 1;4;7
Vậy {x;y} = {1;4;7;0}

a. x4 : xn = x4 - n
b. xn : x5 = xn - 5
c. \(\left(3x^4y^3+\dfrac{1}{2}x^3y^2+x^5y\right):4x^ny^n\)
= \(3x^4y^3:4x^ny^n+\dfrac{1}{2}x^3y^2:4x^ny^n+x^5y:4x^ny^n\)
= \(\dfrac{3}{4}x^{4-n}y^{3-n}+\dfrac{1}{8}x^{3-n}y^{2-n}+\dfrac{1}{4}x^{5-n}y^{1-n}\)

ĐK: \(x-9\ne0\Rightarrow x\ne9\)
\(\sqrt{x}\ge0\Rightarrow x\ge0\)
\(x+\sqrt{x}-6\ne0\Rightarrow x+3\sqrt{x}-2\sqrt{x}-6\ne0\Rightarrow\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)\ne0\)
\(\Rightarrow\sqrt{x}-2\ne0\Rightarrow\sqrt{x}\ne2\Rightarrow x\ne4\)
ĐKXĐ: \(x\ge0;x\ne4;x\ne9\)
\(A=\left(\frac{x-3\sqrt{x}}{x-9}\right):\left(\frac{1}{x+\sqrt{x}-6}+\frac{\sqrt{x}-3}{\sqrt{x}-2}-\frac{\sqrt{x}-2}{\sqrt{x}+3}\right)\)
\(=\frac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}:\left(\frac{1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}+\frac{\sqrt{x}-3}{\sqrt{x}-2}-\frac{\sqrt{x}-2}{\sqrt{x}+3}\right)\)
\(=\frac{\sqrt{x}}{\sqrt{x}+3}:\left(\frac{1+\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)-\left(\sqrt{x}-2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\right)\)
\(=\frac{\sqrt{x}}{\sqrt{x}+3}:\frac{1+x-9-x+4\sqrt{x}-4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\)
\(=\frac{\sqrt{x}}{\sqrt{x}+3}.\frac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}{4\sqrt{x}-12}\)
\(=\frac{\sqrt{x}\left(\sqrt{x}-2\right)}{4\left(\sqrt{x}-3\right)}\)
2, Với \(x=\frac{25}{16}\)\(\Rightarrow\sqrt{x}=\sqrt{\frac{25}{16}}=\frac{5}{4}\)
\(A=\frac{\frac{5}{4}\left(\frac{5}{4}-2\right)}{4\left(\frac{5}{4}-3\right)}=\frac{5}{4}.\left(-\frac{3}{4}\right):4\left(-\frac{7}{4}\right)=-\frac{15}{16}:-7=\frac{15}{112}\)
\(\orbr{\begin{cases}\orbr{\begin{cases}\\\end{cases}}\\\end{cases}}\)\(\orbr{\begin{cases}\orbr{\begin{cases}\sqrt{x}-2< 0\\\sqrt{x}-3>0\end{cases}\Rightarrow\orbr{\begin{cases}\sqrt{x}< 2\\\sqrt{x}>3\end{cases}}\Rightarrow\orbr{\begin{cases}x< 4\\x>9\end{cases}}}\\\orbr{\begin{cases}\sqrt{x}-2>0\\\sqrt{x}-3< 0\end{cases}\Rightarrow\orbr{\begin{cases}\sqrt{x}>2\\\sqrt{x}< 3\end{cases}\Rightarrow\orbr{\begin{cases}x>4\\x< 9\end{cases}}}}\end{cases}}\)
Đặt A = \(\frac{1}{2}\)x5y - \(\frac{3}{4}\)x5y + x5y
Ta có: A = (\(\frac{1}{2}\) - \(\frac{3}{4}\) + 1) x5y
A = \(\frac{3}{4}\) x5y .
Thay x = 1; y = -1 vào A ta được đơn thức: A = \(\frac{3}{4}\) x5y = \(\frac{3}{4}\) 15(-1) = - \(\frac{3}{4}\).
Vậy A = - \(\frac{3}{4}\) tại x = 1 và y = -1.