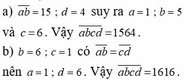Một số có 04 chữ số abcd. Hãy tìm số abcd. Biết rằng:a+b+c+d=19 và nếu chia số đo thành 02 số có 02 chữ số là ab*cd=342 và ab nhỏ hơn cd .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 2 2017
a) a b c d = 15; d = 4 suy ra a = 1; b = 5 và c = 6. Vậy a b c d = 1564.
b) b = 6; c = 1 có a b = c d nên a = 1; d = 6. Vậy a b c d = 1616.
26 tháng 8 2015
abcd=100ab+cd=99ab+ab+cd
99ab chia hết cho 11;ab+cd chia hết cho 11
=>abcd chia hết cho 11
=>đpcm
26 tháng 8 2015
abcd=100ab+cd=99ab+ab+cd
99ab chia hết cho 11;ab+cd chia hết cho 11
=>abcd chia hết cho 11
=>đpcm
HD
0
DN
28 tháng 10 2023
ta có
abcd
= ab. 100 + cd
=8cd . 100 + cd
= cd ( 100.8 + 1)
= cd .801
mà 801 ⋮ 89
=. cd. 801 ⋮ 89
=> abcd ⋮ 89
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
28 tháng 10 2023
\(\overline{abcd}\) = \(\overline{ab}\) x 100 + \(\overline{cd}\)
Thay \(\overline{ab}\) = 8.\(\overline{cd}\) vào biểu thức: \(\overline{abcd}\) = \(\overline{ab}\) x 100 + \(\overline{cd}\) ta có:
\(\overline{abcd}\) = 8.\(\overline{cd}\).100 + \(\overline{cd}\)
\(\overline{abcd}\) = 801.\(\overline{cd}\) = 89.9.\(\overline{cd}\) ⋮ 89 (đpcm)
5 tháng 3 2016
Số abcd chia hết cho tích ab . cd
=> số abcd chia hết cho ab và cd abcd = ab . 100 + cd abcd chia hết cho ab
=> cd chia hết cho ab
=> cd = m.ab ﴾m là chữ số do ab; cd là số có 2 chữ số﴿ abcd chia hết cho cd
=> ab. 100 chia hết cho cd
=> 100.ab = n.cd
=> 100.ab = m.n.ab
=> m.n = 100
=> m = 1; 2; 4; 5;
+﴿ m = 1
=> ab = cd : Số abcd = abab chia hết cho ab.ab
=> 101.ab chia hết cho tích ab.ab
=> 101 chia hết cho ab
=> không có số nào thỏa mãn
+﴿ m = 2
=> cd = 2.ab : số abcd = 100ab + 2ab = 102.ab chia hết cho 2.ab. ab
=> 51 chia hết cho ab
=> ab = 17
=> cd = 34
=> có số 1734
+﴿ m = 4
=> cd = 4.ab : số abcd = 104. ab chia hết cho 4.ab.ab
=> 26 chia hết cho ab
= > ab = 13
=> cd = 52 có Số 1352
+﴿ m = 5
=> cd = 5ab : số abcd = 105 .ab chia hết cho 5.ab.ab
=> 21 chia hết cho ab
=> ab = 21 => cd = 105 Loại
Vậy có 2 số thỏa mãn: 1734 và 1352