Dây dẫn đồng chất tiết diện đều điện trở r = 10Ω được uốn thành một đường tròn kín. Tìm hai điểm A, B trên đường tròn sao cho điện trở giữa chúng bằng 1Ω.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MN
1
TK
27 tháng 9 2021
Đổi 0,2mm2=2.10-7m2
\(R=\dfrac{\rho l}{s}=\dfrac{1,68\cdot10^{-8}\cdot34}{2\cdot10^{-7}}=2,856\left(\Omega\right)\)
HT
31 tháng 12 2020
Ủa điện áp là hiệu điện thế đó :v
\(I=\dfrac{U}{R_1+R_2}=\dfrac{12}{2+10000}=...\left(A\right)\)
\(\Rightarrow U_1=I.R_1=2.I=...\left(V\right);U_2=12-U_1=...\left(V\right)\)
2 tháng 10 2023
Điện trở dây 2 :
\(\dfrac{l_1}{l_2}=\dfrac{R_1}{R_2}\rightarrow R_2=l_2.R_1:l_1=24.3:6=12\left(\Omega\right)\)
VT
16 tháng 6 2018
Đáp án A
Phương pháp: Sử dụng hệ thức của định luật Ôm và công thức tính công suất tiêu thụ
Cách giải:
Giả sử cuộn dây thuần cảm:
Ta có, khi R = R 2 công suất tiêu thụ trên biến trở cực đại
Khi đó ta có: R 2 = | Z L - Z C | = 40 - 25 = 15 W
Mặt khác: P R 2 = U 2 2 R 2 = 120 2 2.15 = 480 ≠ 160
⇒ điều giả sử ban đầu là sai
⇒ Cuộn dây không thuần cảm có điện trở r
- Ta có:
+ Ban đầu khi mắc vào hai đầu A, M một ắc quy có suất điện động E = 12V, điện trở trong r 1 = 4 W thì I 1 = 0 , 1875
Theo định luật Ôm, ta có: I 1 = E R b + r = E R 1 + r + r 1 → R 1 + r 1 + r = E I 1 = 64 → R 1 + r = 60 Ω ( 1 )
+ Khi mắc vào A,B một hiệu điện thế u = 120 2 cos 100 π t , R = R 2 thì công suất tiêu thụ trên biến trở cực đại và bằng 160W
Ta có:
Công suất trên biến trở R đạt cực đại khi R 2 2 = r 2 + Z L − Z C 2 ( 2 )
Mặt khác, ta có:
Công suất trên R 2 : P = U 2 ( R 2 + r ) 2 + Z L − Z C 2 R 2 = 160 W → R 2 ( R 2 + r ) 2 + Z L − Z C 2 = 160 120 2 = 1 90
90 R 2 = 2 R 2 2 + 2 r R → R 2 + r = 45
Kết hợp với (2) ta được: R 2 2 = ( 45 − R 2 ) 2 + 15 2 → R 2 = 25 Ω , r = 20 Ω
Với r = 20W thay vào (1) ⇒ R 1 = 60 - 20 = 40 Ω
→ R 1 R 2 = 40 25 = 1,6
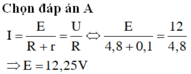
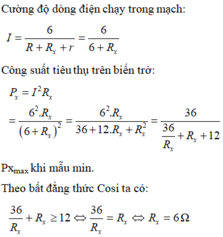
gọi điện trở dây trên điểm A là R1
=>điện trở dây trên điểm B là R2=10-R1(om)
do 2 điện trở này song song
\(=>Rtd=\dfrac{R1\left(10-R1\right)}{R1+10-R1}=\dfrac{10R1-R1^2}{10}=1\)
\(=>-R1^2+10R1=10< =>-R1^2+10R1-10=0\)
\(\Delta=10^2-4\left(-1\right)\left(-10\right)=60>0\)
\(=>\)pt có 2 nghiệm phân biệt R3,R4
\(=>\left[{}\begin{matrix}R3=\dfrac{-10+\sqrt{60}}{2\left(-1\right)}\approx1,13\left(om\right)\\R4=\dfrac{-10-\sqrt{60}}{2\left(-1\right)}\approx8,87\left(om\right)\end{matrix}\right.\)
\(=>\left[{}\begin{matrix}R1=1,13\left(om\right)\\R1=8,87\left(om\right)\end{matrix}\right.\)
\(=>\left[{}\begin{matrix}R2=1,13\left(om\right)\\R2=8,87\left(om\right)\end{matrix}\right.\)
áp dụng \(\dfrac{R1}{R2}=\dfrac{n1}{n2}\)\(=>\left[{}\begin{matrix}\dfrac{n1}{n2}=\dfrac{1,13}{8,87}=\dfrac{113}{887}\\\dfrac{n1}{n2}=\dfrac{8,87}{1,13}=\dfrac{887}{113}\end{matrix}\right.\)
vậy 2 điểm A,B trên đường tròn cần thỏa mãn chiều dài theo tỉ lệ
\(\dfrac{113}{887}\) hoặc \(\dfrac{887}{113}\)