Mọi ngừi ơi giúp mình mấy bài này với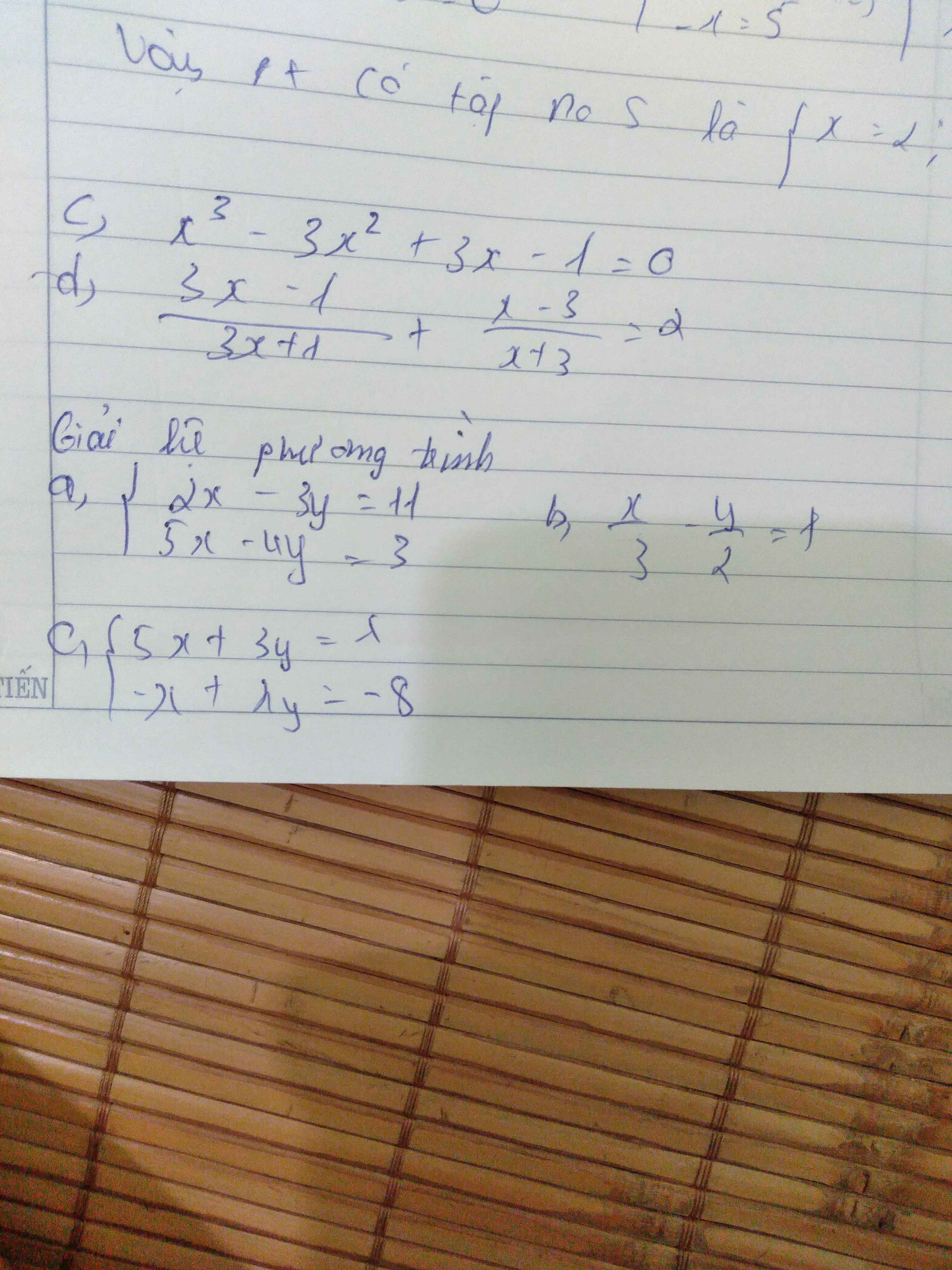
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 6 2021
a) \(\dfrac{2x}{3}\)+\(\dfrac{2x-1}{6}\)=4 - \(\dfrac{x}{3}\)
<=>\(\dfrac{2x}{3}\)+\(\dfrac{2x-1}{6}\) - 4+\(\dfrac{x}{3}\)=0
<=>\(\dfrac{2x.2+2x-1-4.6+x.2}{6}\)=0
=>4x-2x-24+2x=0
<=>4x-24=0
<=>4x=24
<=>x=6
Vậy x=6
15 tháng 6 2021
b)\(\dfrac{x-1}{2}\)+\(\dfrac{x-1}{4}\)=1 - \(\dfrac{2\left(x-1\right)}{3}\)
<=>\(\dfrac{x-1}{2}\)+\(\dfrac{x-1}{4}\)-1+\(\dfrac{2\left(x-1\right)}{3}\)=0
<=>\(\dfrac{6.\left(x-1\right)+3\left(x-1\right)-1.12+4.2\left(x-1\right)}{12}\)=0
=>6x-6+3x-3-12+4x-4+2x-2=0
<=>15x-27=0
<=>15x=27
<=>x=\(\dfrac{9}{5}\)
Vậy x=\(\dfrac{9}{5}\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 8 2021
\(\sqrt{20}-\sqrt{45}+\sqrt{6+2\sqrt{5}}=\sqrt{2^2.5}-\sqrt{3^2.5}+\sqrt{\left(\sqrt{5}+1\right)^2}=2\sqrt{5}-3\sqrt{5}+\sqrt{5}+1=1\)
\(\sqrt{20}-2-\sqrt{\left(\sqrt{5}-2\right)^2}=2\sqrt{5}-2-\left|\sqrt{5}-2\right|=2\sqrt{5}-2-\sqrt{5}+2=\sqrt{5}\)
\(\left(\sqrt{27}+3\sqrt{12}-2\sqrt{3}\right):\sqrt{3}=\left(3\sqrt{3}+6\sqrt{3}-2\sqrt{3}\right):\sqrt{3}=7\sqrt{3}:\sqrt{3}=7\)
\(\sqrt{50}-3\sqrt{8}+\sqrt{\left(\sqrt{2}+1\right)^2}=\sqrt{5^2.2}-3\sqrt{2^2.2}+\sqrt{\left(\sqrt{2}+1\right)^2}=5\sqrt{2}-6\sqrt{2}+\sqrt{2}+1=1\)
2 tháng 8 2021
1) \(A=\sqrt{20}-\sqrt{45}+\sqrt{6+2\sqrt{5}}\)
\(=2\sqrt{5}-3\sqrt{5}+\sqrt{5}+1\)
=1
2) Ta có: \(B=\sqrt{20}-2-\sqrt{\left(\sqrt{5}-2\right)^2}\)
\(=2\sqrt{5}-2-\sqrt{5}+2\)
\(=\sqrt{5}\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 8 2021
1.
a.
ĐKXĐ: \(x^2-1>0\Rightarrow\left[{}\begin{matrix}x>1\\x< -1\end{matrix}\right.\)
\(log_2\left(x^2-1\right)=3\)
\(\Rightarrow x^2-1=8\)
\(\Leftrightarrow x^2=9\)
\(\Rightarrow x=\pm3\) (tm)
b.
ĐKXĐ: \(x>0\)
\(log_3x+log_{\sqrt{3}}x+log_{\dfrac{1}{3}}x=6\)
\(\Leftrightarrow log_3x+2log_3x-log_3x=6\)
\(\Leftrightarrow log_3x=3\)
\(\Rightarrow x=3^3=27\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 8 2021
c. ĐKXĐ: \(x>0\)
\(log_{\sqrt{2}}^2x+3log_2x+log_{\dfrac{1}{2}}x=2\)
\(\Leftrightarrow\left(2log_2x\right)^2+3log_2x-log_2x=2\)
\(\Leftrightarrow4log_2^2x+2log_2x-2=0\)
\(\Rightarrow\left[{}\begin{matrix}log_2x=-1\\log_2x=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\sqrt{2}\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
30 tháng 10 2021
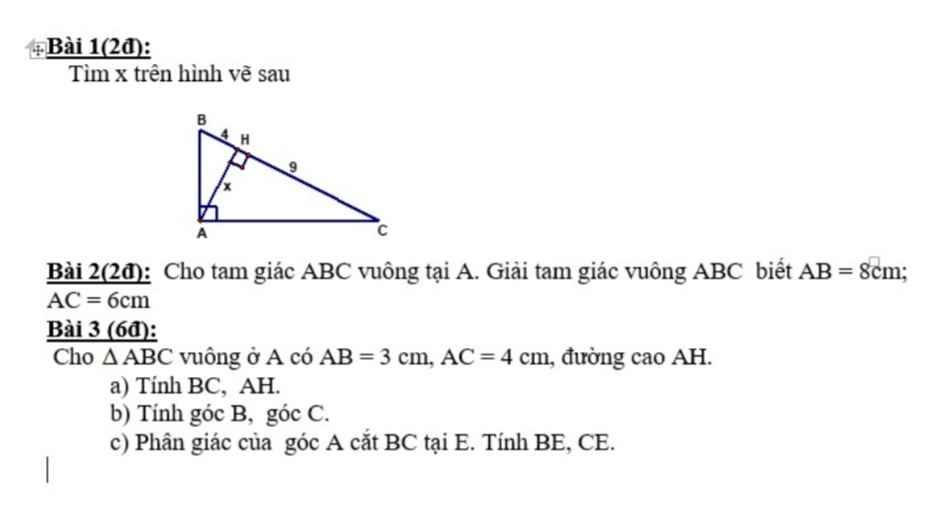
Bài 1:
Áp dụng HTL trong tam giác vuông:
$AH^2=BH.CH$
$\Leftrightarrow x^2=4.9=36$
$\Rightarrow x=6$ (do $x>0$)
AH
Akai Haruma
Giáo viên
30 tháng 10 2021
Bài 2:
Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10$ (cm)
$\sin B=\frac{AC}{BC}=\frac{6}{10}=\frac{3}{5}$
$\Rightarrow \widehat{B}=36,87^0$
$\widehat{C}=90^0-\widehat{B}=90^0-36,87^0=53,13^0$
10 tháng 1 2020
hoạt động dân gian ngày tết có ông địa cầm quạt phe phẩy ?
tôm khô ăn với củ gì vào ngày tết
món này ngày tết,năm quả trên mâm,nhà nào cũng có,vào khắc giao thừa
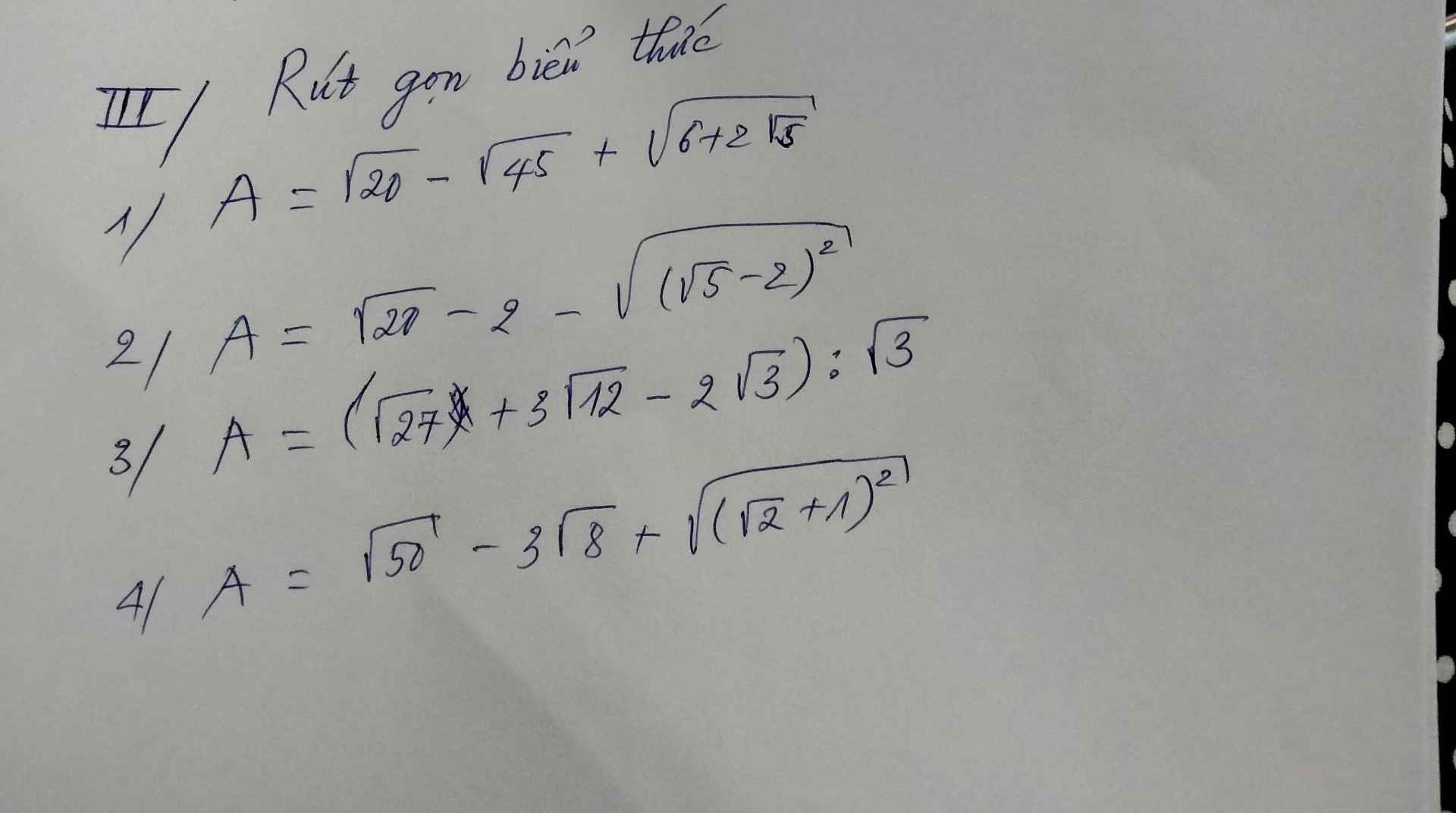
Lời giải.
c.
$x^3-3x^2+3x-1=0$
$\Leftrightarrow (x-1)^3=0$
$\Leftrightarrow x-1=0$
$\Leftrightarrow x=1$
Vậy pt có tập nghiệm $S=\left\{1\right\}$
d. ĐKXĐ: $x\neq \frac{-1}{3}; -3$
PT $\Leftrightarrow \frac{(3x-1)(x+3)+(x-3)(3x+1)}{(3x+1)(x+3)}=2$
$\Leftrightarrow \frac{6x^2-6}{3x^2+10x+3}=2$
$\Leftrightarrow 6x^2-6=2(3x^2+10x+3)$
$\Leftrightarrow 20x+12=0$
$\Leftrightarrow x=\frac{-3}{5}$ (tm)
Vậy tập nghiệm của pt là $S=\left\{\frac{-3}{5}\right\}$
Bài 2:
a.
\(\left\{\begin{matrix} 2x-3y=11\\ 5x-4y=3\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 10x-15y=55\\ 10x-8y=6\end{matrix}\right.\)
\(\Rightarrow (10x-8y)-(10x-15y)=6-55\)
\(\Leftrightarrow 7y=-49\Leftrightarrow y=-7\)
\(x=\frac{3y+11}{2}=\frac{3.(-7)+11}{2}=-5\)
Vậy hpt có nghiệm $(x,y)=(-5,-7)$
b. Không đủ cơ sở để tìm $x,y$
c.
\(\left\{\begin{matrix} 5x+3y=\lambda\\ -x+\lambda y=-8\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 5x+3y=\lambda\\ -5x+5\lambda y=-40\end{matrix}\right.\)
\(\Rightarrow (3+5\lambda)y=\lambda-40\)
Nếu $\lambda = \frac{-3}{5}$ thì $0.y=\frac{-203}{5}$ (vô lý) nên hpt vô nghiệm
Nếu $\lambda \neq \frac{-3}{5}$ thì:
$y=\frac{\lambda - 40}{3+5\lambda}$
$x=8+\lambda y=\frac{\lambda ^2+24}{5\lambda +3}$