Câu 5: C,D

Câu 6; B

Câu 7: A

Câu 8:B

 C,D

 B

 A

B

• Xét bộ ba: 3 c m ,5 c m ,7 c m . Ta có:  3 + 5 = 8 > 7 3 + 7 = 10 > 5 5 + 7 = 12 > 3 (thỏa mãn bất đẳng thức tam giác) nên bộ ba 3 c m ,5 c m ,7 c m lập thành một tam giác nên loại A.

• Xét bộ ba 4 c m ,5 c m ,6 c m . Ta có:  4 + 5 = 9 > 6 4 + 6 = 10 > 5 5 + 6 = 11 > 4 (thỏa mãn bất đẳng thức tam giác) nên bộ ba  4 c m ,5 c m ,6 c m lập thành một tam giác nên loại B.

• Xét bộ ba 3 c m ,6 c m ,5 c m . Ta có:  3 + 6 = 9 > 5 3 + 5 = 8 > 6 6 + 5 = 11 > 3 (thỏa mãn bất đẳng thức tam giác) nên bộ ba  3 c m ,6 c m ,5 c m lập thành một tam giác nên loại D.

• Xét bộ ba 2 c m ,5 c m ,7 c m . Ta có:  2 + 5 = 7 (không thỏa mãn bất đẳng thức tam giác) nên bộ ba  2 c m ,5 c m ,7 c m không lập thành một tam giác nên chọn C.

Chọn đáp án C.

Ta có : 4cm + 3cm = 7cm > 6cm.

⇒ Bộ ba đoạn thẳng 3cm, 4cm, 6cm thỏa mãn bất đẳng thức tam giác nên là ba cạnh của tam giác.

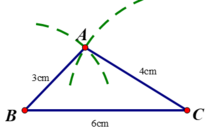
Cách dựng tam giác có ba độ dài 3cm, 4cm, 6cm

- Vẽ BC = 6cm

- Dựng đường tròn tâm B bán kính 3cm ; đường tròn tâm C bán kính 4cm. Hai đường tròn cắt nhau tại A. Nối AB, AC ta được tam giác cần dựng.

Vì 6cm = 2cm + 4cm

⇒ Bộ ba đoạn thẳng 2cm, 4cm, 6cm không thỏa mãn bất đẳng thức tam giác nên không phải là ba cạnh của tam giác.

Ta có: 3cm + 2cm = 5cm < 6cm

⇒ Bộ ba đoạn thẳng 2cm, 3cm, 6cm không thỏa mãn bất đẳng thức tam giác nên không phải là ba cạnh của tam giác.

Vì 6+8=14>10 không thỏa mãn bất đẳng thức tam giác. Chọn A

a

Giúp mình với!!!

Bài 40:

a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có 

BD chung

\(\widehat{ABD}=\widehat{EBD}\)

Do đó: ΔABD=ΔEBD

Suy ra: BA=BE và DA=DE

Ta có: BA=BE

nên B nằm trên đường trung trực của AE(1)

Ta có: DA=DE

nên D nằm trên đường trung trực của AE(2)

Từ (1) và (2) suy ra BD là đường trung trực của AE

b: Xét ΔADF vuông tại A và ΔEDC vuông tại E có

DA=DE

\(\widehat{ADF}=\widehat{EDC}\)

Do đó: ΔADF=ΔEDC

Suy ra: DF=DC

c: Ta có: AD=DE

mà DE<DC

nên AD<DC

d: Ta có: ΔADF=ΔEDC

nên AF=EC

Xét ΔBFC có 

\(\dfrac{BA}{AF}=\dfrac{BE}{EC}\)

Do đó: AE//CF

a) Vì 7 + 8 > 11       

Nên a là một tam giác theo bất đẳng thức tam giác

b) Vì 7 + 9 = 16 không thỏa mãn bất đẳng thức tam giác nên b không phải là tam giác

c) Vì 8 + 9 > 16

Nên c là một tam giác theo bất đẳng thức tam giác

Theo bất đẳng thức tam giác:

a) Ta xét :

4 + 5 > 7

4 + 7 > 5

5 + 7 > 4

\( \Rightarrow \) Cả 3 cạnh của tam giác đều thỏa mãn bất đẳng thức tam giác

\( \Rightarrow \) a là tam giác

b) Ta xét :

2 + 4 = 6

\( \Rightarrow \)  Cả 3 cạnh của tam giác không thỏa mãn bất đẳng thức tam giác

\( \Rightarrow \) b không là tam giác

c) Ta xét :

3 + 4 < 8

\( \Rightarrow \) Cả 3 cạnh của tam giác không thỏa mãn bất đẳng thức tam giác

\( \Rightarrow \) c không là tam giác