Giaỉ phương trình : 6x4 + 5x3 -38x2 + 5x +6=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


f ) \(\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)-24\)
\(=\left[\left(x+1\right)\left(x+4\right)\right]\left[\left(x+2\right)\left(x+3\right)\right]-24\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)-24\)
Đặt \(x^2+5x+5=t\), ta có :
\(\left(t-1\right)\left(t+1\right)-24\)
\(=t^2-1-24=t^2-25\)
\(=\left(t-5\right)\left(t+5\right)\)
Thay và ta có :
\(\left(x^2+5x+5-5\right)\left(x^2+5x+5+5\right)\)
\(=\left(x^2+5x\right)\left(x^2+5x+10\right)\)
\(=x\left(x+5\right)\left(x^2+5x+10\right)\)

5x3 – x2 – 5x + 1 = 0
⇔ x2(5x – 1) – (5x – 1) = 0
⇔ (x2 – 1)(5x – 1) = 0
⇔ (x – 1)(x + 1)(5x – 1) = 0
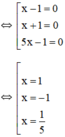
Vậy phương trình có tập nghiệm 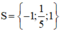

a) 1,2x3 – x2 – 0,2x = 0
⇔ 0,2x.(6x2 – 5x – 1) = 0
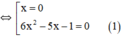
Giải (1): 6x2 – 5x – 1 = 0
có a = 6; b = -5; c = -1
⇒ a + b + c = 0
⇒ (1) có hai nghiệm x1 = 1 và x2 = c/a = -1/6.
Vậy phương trình ban đầu có tập nghiệm 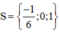
b) 5x3 – x2 – 5x + 1 = 0
⇔ x2(5x – 1) – (5x – 1) = 0
⇔ (x2 – 1)(5x – 1) = 0
⇔ (x – 1)(x + 1)(5x – 1) = 0
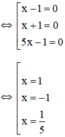
Vậy phương trình có tập nghiệm 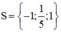

a: Ta có: x+17<10
nên x<-7
b: Ta có: 9-2x<0
\(\Leftrightarrow2x>9\)
hay \(x>\dfrac{9}{2}\)
c: Ta có: \(-3x-11\ge0\)
\(\Leftrightarrow-3x\ge11\)
hay \(x\le-\dfrac{11}{3}\)

Ta co:6ax^2+4ax—9x—6=0
«=»2ax(3x+2)—3(3x+2)=0
«=»(3x+2)(2ax—3)=0
các bục sau tu giai
ta có : 6ax2+4ax-9x-6=0
\(\Leftrightarrow\)2ax(3x+2)-3(3x+2)=0
\(\Leftrightarrow\)(3x+2)(2ax-3)=0
xét 3x+2=0\(\Rightarrow\)x=\(\frac{-2}{3}\)
thay x vừa tìm được vào ta tính được a=\(\frac{-13}{3}\)

a. \(\Leftrightarrow2x\ge10\Leftrightarrow x\ge5\)
b.\(-5x-1\le x+5\Leftrightarrow-6\le6x\Leftrightarrow x\ge-1\)

`a,4x^2+(x-1)^2-(2x+1)^2=0`
`<=>4x^2+3x(-x-2)=0`
`<=>x(4x-3x-6)=0`
`<=>x(x-6)=0`
`<=>` $\left[ \begin{array}{l}x=0\\x=6\end{array} \right.$
`b)(x^2-3x)^2+5(x^2-3x)+6=0`
Đặt `x^2-3x=a(a>=-9/4)`
`pt<=>a^2+5a+6=0`
`<=>(a+2)(a+3)=0`
`<=>` $\left[ \begin{array}{l}a=-2\\a=-3(l)\end{array} \right.$
`<=>x^2-3x=-2`
`<=>x^2-3x+2=0`
`<=>(x-1)(x-2)=0`
`<=>` $\left[ \begin{array}{l}x=2\\x=1\end{array} \right.$
Ta có : \(6x^4+5x^3-38x^2+5x+6=0\)
\(\Leftrightarrow6x^4+20x^3+6x^2-15x^3-50x^2-15x+6x^2+20x+6=0\)
\(\Leftrightarrow2x^2\left(3x^2+10x+3\right)-5x\left(3x^2+10x+3\right)+2\left(3x^2+10x+3\right)=0\)
\(\Leftrightarrow\left(3x^2+10x+3\right)\left(2x^2-5x+2\right)=0\)
\(\Leftrightarrow\left(3x^2+x+9x+3\right)\left(2x^2-x-4x+2\right)=0\)
\(\Leftrightarrow\left[x\left(3x+1\right)+3\left(3x+1\right)\right]\left[x\left(2x-1\right)-2\left(2x-1\right)\right]=0\)
\(\Leftrightarrow\left(3x+1\right)\left(x+3\right)\left(2x-1\right)\left(x-2\right)=0\)
\(\Leftrightarrow\)\(3x+1=0\)
hoặc \(x+3=0\)
hoặc \(2x-1=0\)
hoặc \(x-2=0\)
\(\Leftrightarrow\)\(x=-\frac{1}{3}\)
hoặc \(x=-3\)
hoặc \(x=\frac{1}{2}\)
hoặc \(x=2\)
Vậy tập nghiệm của phương trình là \(S=\left\{-\frac{1}{3};-3;\frac{1}{2};2\right\}\)