giúp em bài này nhé
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: \(H=6x^3y^4-2x^4y^2+3x^2y^2+5x^4y^2-a\cdot x^3y^4\)
\(=\left(6x^3y^4-a\cdot x^3y^4\right)+3x^2y^2+3x^4y^2\)
\(=x^3y^4\left(6-a\right)+3x^2y^2+3x^4y^2\)
Để bậc của đa thức H bằng 6 thì 6-a=0
=>a=6
b: Khi a=6 thì \(H=3x^2y^2+3x^4y^2\)
\(=3x^2y^2\left(x^2+1\right)\)
Khi x<>0 và y<>0 thì \(x^2>0;y^2>0;x^2+1>1>0\)
=>\(x^2\cdot y^2\left(x^2+1\right)>0\)
=>\(H=3\cdot x^2y^2\left(x^2+1\right)>0\forall x,y\ne0\)


\(1,=\left(\dfrac{11}{24}+\dfrac{13}{24}\right)-\left(\dfrac{5}{41}+\dfrac{36}{41}\right)+0,5=1-1+0,5=0,5\\ 2,=-12:\left(-\dfrac{1}{12}\right)^2=12\cdot\dfrac{1}{144}=\dfrac{1}{12}\\ 3,=\dfrac{7}{23}\left(-\dfrac{23}{6}\right)=-\dfrac{7}{6}\\ 4,=\dfrac{7}{5}\left(23\dfrac{1}{4}-13\dfrac{1}{4}\right)=\dfrac{7}{5}\cdot10=14\\ 5,=\dfrac{17}{12}\cdot\left(\dfrac{4}{5}-\dfrac{3}{4}\right)^2=\dfrac{17}{12}\cdot\left(\dfrac{1}{20}\right)^2=\dfrac{17}{12}\cdot\dfrac{1}{400}=\dfrac{17}{4800}\\ 6,=\dfrac{5}{3}\left(-16\dfrac{2}{7}+28\dfrac{2}{7}\right)=\dfrac{5}{3}\cdot12=20\\ 7,=\left(3-\dfrac{1}{2}\right)\cdot\dfrac{6}{5}-17=\dfrac{5}{2}\cdot\dfrac{6}{5}-17=-14\\ 8,=\left[\dfrac{1}{9}\cdot\left(-9\right)\right]^{25}-\dfrac{2}{3}\cdot\dfrac{1}{4}=-1-\dfrac{1}{6}=-\dfrac{7}{6}\)
\(9,=\dfrac{3}{5}:\left(-\dfrac{7}{30}\right)+\dfrac{3}{5}:\left(-\dfrac{7}{5}\right)=\dfrac{3}{5}\left(-\dfrac{30}{7}-\dfrac{5}{7}\right)=\dfrac{3}{5}\left(-5\right)=-3\\ 10,=5,7\cdot\left(-10\right)=-57\\ 11,=10\cdot\dfrac{1}{10}\cdot\dfrac{4}{3}+21-\dfrac{1}{3}=\dfrac{4}{3}-\dfrac{1}{3}+21=1+21=22\\ 12,=\dfrac{2^{10}}{2^{10}}-\dfrac{2^5\cdot3^3\cdot5^3}{2^3\cdot3^3\cdot2^2\cdot5^2}=5\)


\(\Delta'=4-\left(m-1\right)=5-m\)
để pt có nghiệm kép khi \(5-m=0\Leftrightarrow m=5\)
chọn B
Phương trình có nghiệm kép khi:
\(\Delta'=4-\left(m-1\right)=0\Leftrightarrow5-m=0\)
\(\Rightarrow m=5\)

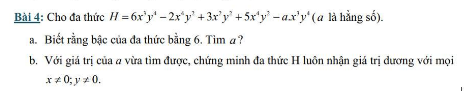

 Giải giúp em mấy bài toán này, gấp nhé. Em cảm ơn
Giải giúp em mấy bài toán này, gấp nhé. Em cảm ơn