Cho tứ diện ABCD. Gọi \(G_1;G_2;G_3\) lần lượt là trọng tâm của các tam giác ABC, ACD, ABD. Chứng minh rằng \(\left(G_1G_2G_3\right)\) // (BCD)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
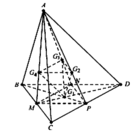
Ta có d G 1 ; G 2 G 3 G 4 = 1 2 d A ; G 2 G 3 G 4
= 1 2 . 2 3 d A ; M N P = 1 3 d A ; M N P S G 2 G 3 G 4 = 2 3 2 S M N P = 4 9 . 1 4 S A B C = 1 9 S A B C
Thể tích của khối tứ diện G 1 G 2 G 3 G 4 là
V = 1 3 d G 1 ; G 2 G 3 G 4 . S G 2 G 3 G 4 = 1 3 . 1 3 . d A ; M N P . 1 9 S A B C = 1 27 V A B C D = V 27

Đáp án: A.
§ Hướng dẫn giải:
Dễ dàng ta có được
V A B ' C ' D V A B C D = A B ' A B . A C ' A C = 1 4

Đáp án B
Ta có:
V M N P Q V A B C D = 1 3 . 1 3 2 = 1 27 ⇒ V M N P Q = V A B C D 27 = 9 3 27 = 3 3 c m 3




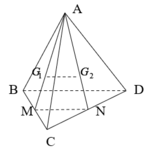
Gọi I, J và K lần lượt là trung điểm của các cạnh BC, CD và BD. Theo tính chất trọng tâm của tam giác ta có :