a) HS tự biểu diễn. b) Các số nguyên âm gồm có: -4; -3; -2. HS tự biểu diễn. c) Không

a) Biểu diễn các số –2; 0; 1; 2 trên trục số.

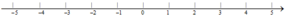
b) Ghi các số nguyên âm nằm giữa các số –4 và –1 trên trục số.

c) Trên trục số không có điểm nào biểu diễn số nguyên âm nằm giữa –2 và –1

a) Biểu diễn các số –3; –4; 2; 4 trên trục số.

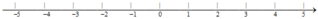
b) Ghi các số nguyên âm nằm giữa các số –5 và –1 trên trục số.

c) Trên trục số không có điểm nào biểu diễn số nguyên âm nằm giữa –5 và –4

Chọn A

Thanks

a)

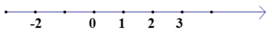
b) Sắp xếp theo thứ tự giảm dần: 3;2;1;-2

c) Số liền sau – 2 là – 3; số liền trước 1 là 0.

-----|-----|-----|-----|-----|-----|-----|----->

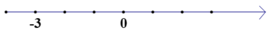
     -3     -2      -1        0      1       2       3

- Biểu diễn số -1: Từ vạch số 0, ta di chuyển 1 vạch về bên trái số 0.

- Biểu diễn số - 5: Từ vạch số 0, ta di chuyển 5 vạch về bên trái số 0.

- Biểu diễn số 1: Từ vạch số 0, ta di chuyển 1 vạch về bên phải số 0. 

- Biểu diễn số 5: Từ vạch số 0, ta di chuyển 5 vạch về bên phải số 0.

- Biểu diễn số - 4: Từ vạch số 0, ta di chuyển 4 vạch về bên trái số 0.

Ta được:

Để biểu diễn phân số 6/11 trên trục số, ta chia đoạn từ 0 đến 1 thành 11 phần bằng nhau. Sau đó, ta điểm trên trục số tương ứng với phần số 6/11 là điểm nằm ở vị trí thứ 6.

Vậy, biểu diễn phân số 6/11 trên trục số là điểm nằm ở vị trí thứ 6 trên đoạn từ 0 đến 1.