 Help ,e
Help ,e
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3:
a: 5^n luôn có chữ số tận cùng là 5 với mọi n là số tự nhiên
=>5^100 có chữ số tận cùng là 5
b: \(2^{4k}\) có chữ số tận cùng là 6 với mọi k là số tự nhiên
mà 100=4*25
nên 2^100 có chữ số tận cùng là 6
c: 2023 chia 2 dư 1
mà \(9^{2k+1}\) luôn có chữ số tận cùng là 9
nên \(9^{2023}\) có chữ số tận cùng là 9
d: 2023 chia 4 dư 3
\(7^{4k+3}\left(k\in N\right)\) luôn có chữ số tận cùng là 3
Do đó: \(7^{2023}\) có chữ số tận cùng là 3
Quy luật:
+) các số có c/s tận cg là 0,1,5,6 nâng lên lũy thừa bậc nào (≠0) thì c/s tận cg vẫn là nó.
+) các số có tận cg là 2,4,8 nâng lên lt bậc 4n(n≠0) thì đều có c.s tận cg là 6.
+)các số có c/s tận cg là 3,7,9 nâng lên lt bậc 4n(n≠0) thì đều có c/s tận cg là 1.
+) số có tận cg là 3 khi nâng lên lũy thừa bậc 4n+3 sẽ có tận cùng là 7
+) số có tận cg là 7 khi nâng lên lũy thừa bậc 4n+3 sẽ có tận cùng là 3
+) số có tận cg là 2 khi nâng lên lũy thừa bậc 4n+3 sẽ có tận cùng là 8
+) số có tận cg là 8 khi nâng lên lũy thừa bậc 4n+3 sẽ có tận cùng là 2
+) số có c/s tận cg là 0,1,4,5,6,9 khi nâng lên lũy thừa bậc 4n+3 thì c/s tận cg là chính nó
Bài 3: áp dụng quy luật bên trên
\(a.5^{100}=\overline{..5}\)
\(b.2^{100}=2^{4.25}=\overline{..6}\)
\(c.9^{2023}=\overline{..9}\)
\(d.7^{2023}=7^{4.505+3}=\overline{...3}\)
Bài 4:
\(A=17^{2008}-11^{2008}-3^{2008}\)
\(=\left(\overline{...7}\right)^{4.502}-\left(\overline{..1}\right)^{2008}-\left(\overline{..3}\right)^{4.502}\)
\(=\overline{..1}-\overline{...1}-\overline{...1}\)
\(=\overline{..9}\)
Bài 5:
\(M=17^{25}+24^4-13^{21}\)
\(=\left(\overline{..7}\right)^{4.6}.\left(\overline{..7}\right)+\left(\overline{..4}\right)^{4.1}-\left(\overline{..3}\right)^{4.5}.\left(\overline{..3}\right)\)
\(\overline{..1}.\overline{..7}+\overline{..6}-\overline{..1}.\overline{..3}\)
\(=\overline{...7}+\overline{..6}-\overline{..3}\)
\(=\overline{...0}\)
\(=>M⋮10\)

Bài 1
a) \(2^{11}.64=2^{11}.2^6=2^{17}\)
Do \(16< 17\Rightarrow2^{16}< 2^{17}\)
Vậy \(2^{16}< 2^{11}.64\)
b) Do \(18>17\Rightarrow9^{18}>9^{17}\) (1)
\(9^{18}=\left(3^2\right)^{18}=3^{36}\)
Do \(36< 37\Rightarrow3^{36}< 3^{37}\)
\(\Rightarrow9^{18}< 3^{37}\) (2)
Từ (1) và (2) \(\Rightarrow9^{17}< 3^{37}\)
c) \(2^{333}=\left(2^3\right)^{111}=8^{111}\)
\(3^{222}=\left(3^2\right)^{111}=9^{111}\)
Do \(8< 9\Rightarrow8^{111}< 9^{111}\)
Vậy \(2^{333}< 3^{222}\)
d) \(3^{50}=\left(3^2\right)^{25}=9^{25}\)
Do \(9< 11\Rightarrow9^{25}< 11^{25}\)
Vậy \(3^{50}< 11^{25}\)
e) \(37< 38\Rightarrow3^{37}< 3^{38}\) (1)
Lại có: \(3^{38}=3^{2.19}=\left(3^2\right)^{19}=9^{19}\)
Do \(9< 10\Rightarrow9^{19}< 10^{19}\)
\(\Rightarrow3^{38}< 10^{19}\) (2)
Từ (1) và (2) \(\Rightarrow3^{37}< 10^{19}\)
f) Do \(17>16\Rightarrow17^{14}>16^{14}\) (1)
Do \(32>31\Rightarrow32^{11}>31^{11}\) (2)
Lại có:
\(16^{14}=\left(2^4\right)^{14}=2^{56}\)
\(32^{11}=\left(2^5\right)^{11}=2^{55}\)
Do \(56>55\Rightarrow2^{56}>2^{55}\)
\(\Rightarrow16^{14}>32^{11}\) (3)
Từ (1), (2) và (3) \(\Rightarrow17^{14}>31^{11}\)
Bài 2:
a) \(2^n-64=0\)
\(2^n=64\)
\(2^n=2^6\)
\(n=6\)
b) \(5.3^{n-3}-405=0\)
\(5.3^{n-3}=405\)
\(3^{n-3}=405:5\)
\(3^{n-3}=81\)
\(n-3=4\)
\(n=4+3\)
\(n=7\)
c) \(4^n.8=2^{15}\)
\(\left(2^2\right)^n.2^3=2^{15}\)
\(2^{2n}.2^3=2^{15}\)
\(2^{2n+3}=2^{15}\)
\(2n+3=15\)
\(2n=15-3\)
\(2n=12\)
\(n=12:2\)
\(n=6\)
d) \(3.2^{n+1}+2^{n+2}=160\)
\(2^{n+1}.\left(3+2\right)=160\)
\(2^{n+1}.5=160\)
\(2^{n+1}=160:5\)
\(2^{n+1}=32\)
\(2^{n+1}=2^5\)
\(n+1=5\)
\(n=5-1\)
\(n=4\)

1, introduce => introduced
2, were => are
3, I => me
4, selled => sold
5, red => read
6, photoes => photos
7, every day by my parents => by my parents every day
8, watch and play => watched and played
9, practices => practiced
10, every afternoon by children => by children every afternoon
11, eat => eaten
12, Are => Is

Câu : \(5\) :
Khuyên chúng ta sống không chỉ biết nhận mà còn phải biết cho .
Câu \(6\) :
Dấu gạch thứ nhất : Đánh dấu chỗ bắt đầu lời nói của nhân vật
Đáp án : A - 2
Dấu gạch ngang thứ hai : Đánh dấu phần chú thích .
Đáp án : B - 1
~ chúc em học tốt ~


Câu 2)
b, Công thực hiện là
\(A=P.h=10m.h=10.6.12=720J\)
a, Phụ thuộc vào khối lượng và quãng đường vật di chuyển
A = F.s
A : công cần tính ( đơn vị J(Jun) ; 1kJ (ki lô jun)= 1000J)
F : lực vật tác động
s : quãng đường vật di chuyển
Câu 3)
Để tính công thực hiện trong 1s
P = A/t
P : công suất ( đơn vị W (oát) -1MGW = 1000kW = 1,000,000W)
A : công
t : thời gian (đơn vị giây)
b, Công suất thực hiện là
\(P=\dfrac{A}{t}=\dfrac{P.h}{t}=\dfrac{10m.h}{t}\\ =\dfrac{10.50.8}{50}=80W\)
Câu 4)
5p = 300s
10p = 600s
Công suất leo của Hương là
\(P=\dfrac{A}{t}=\dfrac{P.h}{t}\\ =\dfrac{10m.h}{t}=\dfrac{10.40.6}{300}=8W\)
Công suất leo của Lan là
\(P=\dfrac{10m.h}{t}=\dfrac{10.50.9}{600}=7,5W\)
Hương leo khoẻ hơn do 8 W > 7,5 W

`#3107.101107`
c)
Ta có:
`2x = 3y`
`=> x/3 = y/2 => x/15 = y/10`
`4y = 5z`
`=> y/5 = z/4 => y/10 = z/8`
`=> x/15 = y/10 = z/8`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/15 = y/10 = z/8 = (x - y - z)/(15 - 10 - 8) = (-27)/(-3) = 27/3 = 9`
`=> x/15 = y/10 = z/8 = 9`
`=>`\(x=15\cdot9=135\\ y=9\cdot10=90\\ z=8\cdot9=72\)
Vậy, giá trị của `x; y; z` lần lượt là `135; 90; 72`
d)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`(x - 5)/3 = (y - 4)/2 = (x - 5 + y - 4)/(3 + 2) = (x + y - 5 - 4)/5 = (-1-9)/5 = (-10)/5 = -2`
`=> (x - 5)/3 = (y - 4)/2 = -2`
`=>`
\(x=\left(-2\cdot3\right)+5=-1\)
\(y=\left(-2\cdot2\right)+4=0\)
Vậy, giá trị của `x; y` lần lượt là `-1; 0`
e)
`(x - 1)/2 = (y - 2)/3 = (z - 3)/4`
`=> (x - 1)/2 = (2y - 4)/6 = (3z - 9)/12`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`(x - 1)/2 = (2y - 4)/6 = (3z - 9)/12 = (x - 1 - (2y - 4) + 3z - 9)/(2 - 6 + 12) =`\(\dfrac{x-1-2y+4+3z-9}{8}=\dfrac{x-2y+3z+\left(-1+4-9\right)}{8}\\ =\dfrac{-10-6}{8}=\dfrac{-16}{8}=-2\)
`=> (x - 1)/2 = (y - 2)/3 = (z - 3)/4 = -2`
`=>`\(x=\left(-2\cdot2\right)+1=-3\); \(y=\left(-2\cdot3\right)+2=-4\); \(z=\left(-2\cdot4\right)+3=-5\)
Vậy, giá trị của `x; y; z` lần lượt là `-3; -4; -5.`

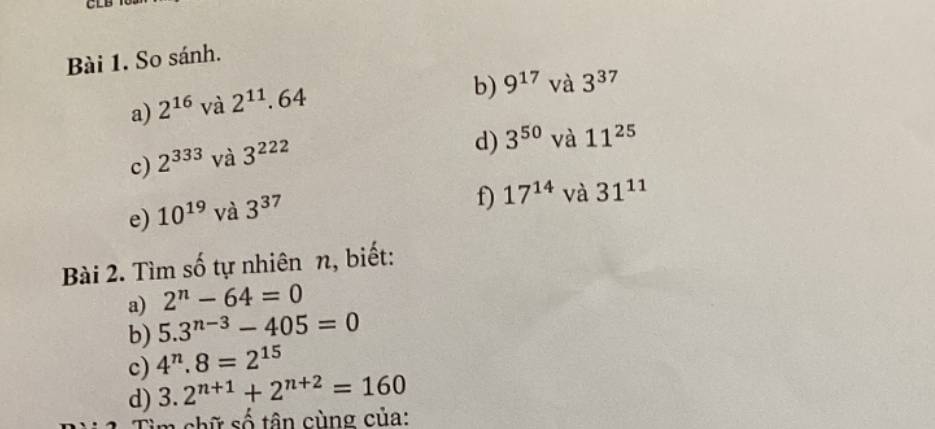




 can you help e?pls
can you help e?pls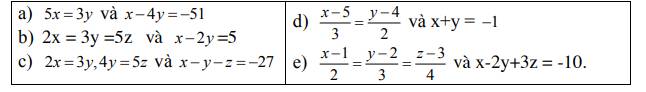
(29) did you do
(30) spent
(31) had just returned
(32) have never been
(33) lived
(34) Are you enjoying
(35) is
(36) don't have
(37) Do you decide
(38) already invited