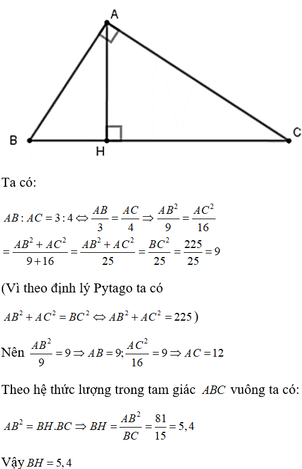
Cho tam giác ABC vuông tại A, \(AH\perp BC\)(H thuộc BC). Cho biết AB : AC=3 : 4 và BC =15cm. Tính độ dài các đoạn thẳng BH và CH.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có AB : AC = 3 : 4 ⇔ A B 3 = A C 4 ⇒ A B 2 9 = A C 2 16
= A B 2 + A C 2 9 + 16 = A B 2 + A C 2 25 = B C 2 25 = 225 25 = 9
(Vì theo định lý Py-ta-go ta có A B 2 + A C 2 = B C 2 ⇔ A B 2 + A C 2 = 225 )
Nên A B 2 9 = 9 ⇒ AB = 9; A C 2 9 = 9 ⇒ AC = 12
Theo hệ thức lượng trong tam giác vuông ABC ta có:
A B 2 = B H . B C ⇒ B H = A B 2 B C = 81 15 = 5 , 4
Vậy BH = 5,4
Đáp án cần chọn là: A

Đặt AB = 3k; AC = 4k . Áp dụng hệ thức lượng vào tam giác vuông ABC thu được k = 3. Từ đó tính được : BH = 5,4cm, HC = 9,6cm

a, HB = 1,8cm; CH = 3,2cm; AH = 2,4cm; AC = 4cm
b, AB = 65cm; AC = 156cm; BC = 169cm; BH = 25cm
c, AB = 5cm; BC = 13cm; BH = 25/13cm; CH = 144/13cm

Áp dụng định lý Py - ta - Go vào tam giác ABC vuông tại A có :
AC2 = BC2 - AB2
AC2 =
Ta có :
Mà :
⇒
⇔ AH =
a) Áp dụng pi ta go ta có : AB2 = AH2 + BH2 = 162 + 252 = 881
=> AB =
Lại có : BH.HC = AH2
<=> HC.25 = 162
<=> HC.25 = 256
<=> HC = 256 : 25 = 10,24
Ta có : BC = HC + BH = 10,24 + 25 = 35,24
Áp dụng bi ta go : AC2 = AH2 + HC2 = 162 + 10,242 = 360,8576
=> AC =

bài 9
tam giác ABC vuông tại A có
* BC2=AB2+AC2
BC2=152+202=625
BC=25cm
* AH.BC=AB.AC
AH.25=15.20
AH.25=300
AH=12cm
tam giác ABH vuông tại H có
BH2=AB2-AH2
BH2=152-122=81
BH=9cm
tam giác ABC vuông tại A có
*AB2=BH.BC
225=9.BC
BC=25cm
CH=BC-BH=25-9=16cm
*AC2=BC2-AB2
AC2=252-152=400
AC=20cm

AB/AC=3/4
=>BH/CH=9/16
=>BH/9=CH/16=(BH+CH)/(9+16)=15/25=0,6
=>BH=5,4cm; CH=9,6cm

a, HB = 1,8cm; CH = 3,2cm; AH = 2,4cm; BC = 5cm
b, AB = 15cm; AC = 20cm; AH = 12cm; BC = 25cm

Ta có : \(\frac{AB}{AC}=\frac{3}{4}\Rightarrow AB=\frac{3}{4}AC\)
Theo định lí Pytago tam giác ABC vuông tại A
\(AB^2+AC^2=BC^2\Rightarrow\left(\frac{3}{4}AC\right)^2+AC^2=225\Rightarrow AC=12\)cm
\(\Rightarrow AB=\frac{3}{4}AC=\frac{3}{4}.12=9\)cm
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thúc : \(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{81}{15}=\frac{27}{5}\)cm
\(\Rightarrow CH=BC-BH=15-\frac{27}{5}=\frac{48}{5}\)cm