Ta có M ∈ O y  nên M(0; m) và  M A → = 1 ; −   1 − m M B → = 3 ; 2 − m .

Khi đó  M A 2 + M B 2 = M A → 2 + M B → 2 = 1 2 + − 1 − m 2 + 3 2 + 2 − m 2 = 2 m 2 − 2 m + 15.

= 2 m − 1 2 2 + 29 2 ≥ 29 2 ;    ∀ m ∈ ℝ .

Suy ra M A 2 + M B 2 min = 29 2 .  

Dấu =  xảy ra khi và chỉ khi m = 1 2    ⇒    M 0 ; 1 2 .  

Chọn C.

M thuộc trục tung nên tung độ y bằng 0

\(\Rightarrow M\left(a;0\right)\)

Ta có P= \(MA^2+MB^2=\sqrt{\left(1-a\right)^2+\left(-1\right)^2}^2+\sqrt{\left(3-a\right)^2+2^2}^2=2a^2-8a+15=2\left(a-2\right)^2+7\ge7\)

\(\Rightarrow\) MinP=7 đạt được khi a=2

khi đó M(2;0)

M thuộc trục tung thì M có toạ độ M(0,a) chứ 

Chọn A

Phương pháp: 

+) Xác định điểm I thỏa mãn   I A → + I B → - I C → = 0 →

+) Khi đó 

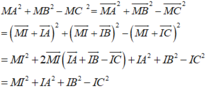
 nhỏ nhất khi và chỉ khi MI ngắn nhất ⇔  M là hình chiếu vuông góc của I lên (Oxy) .

Cách giải:

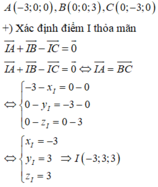
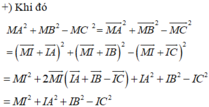
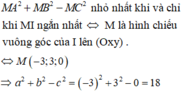
Chọn C

Gọi I là trung điểm của AB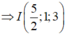 

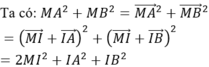
Suy ra: MA² + MB²  đạt giá trị nhỏ nhất khi MI đạt giá trị nhỏ nhất.

=>M là hình chiếu của I trên trục Oz => M (0 ; 0 ; 3)

Đáp án C.

Chọn A.

Phương pháp: 

Đáp án D.

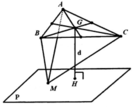
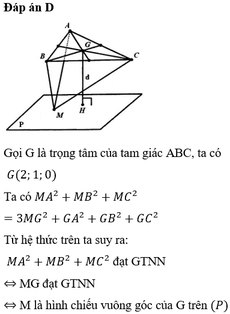
Gọi G là trọng tâm của tam giác ABC, ta có G(2;1;0) 

Ta có:

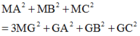
Từ hệ thức trên ta suy ra: M A 2 + M B 2 + M C 2  đạt GTNN

⇔ MG đạt GTNN ⇔ M là hình chiếu vuông góc của G trên (P)

Gọi (d) là đường thẳng qua G và vuông góc với (P) thì (d) có phương trình tham số là 

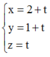
Tọa độ điểm M là nghiệm của hệ phương trình:

Gọi \(M\left(0;m\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(-1;m+2\right)\\\overrightarrow{AB}=\left(-5;7\right)\end{matrix}\right.\)

3 điểm M;A;B thẳng hàng khi:

\(\dfrac{-1}{-5}=\dfrac{m+2}{7}\Rightarrow m=-\dfrac{3}{5}\)

\(\Rightarrow M\left(0;-\dfrac{3}{5}\right)\)