B=32009.72010.132011.Tìm chữ số hàng đơn vị của B
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số thứ nhất là ABCD.
Theo điều kiện, ta có:
- Số thứ hai là ABC.
- Số thứ ba là AB.
- Số thứ tư là A.
Từ đó, ta có hệ phương trình: A + B + C + D = 200
A + B + C = 10A + B = 10B + C = D
Ta thử các giá trị của A từ 1 đến 9:
- Khi A = 1, ta có B + C = 11 và D = 11. Nhưng B và C không thể có tổng là 11.
- Khi A = 2, ta có B + C = 22 và D = 22. Nhưng B và C không thể có tổng là 22.
- ...
- Khi A = 9, ta có B + C = 99 và D = 99. Nhưng B và C không thể có tổng là 99.
Vậy không có 4 số tự nhiên thỏa mãn yêu cầu bài toán.

a)
Số cần tìm bằng thương phép chia 1794 : 9 nhân với 10 rồi cộng với số dư.
1794 : 9 = 199 (dư 3)
Số cần tìm là 199 x 10 + 3 = 1993
b)
Gọi số đó là Ab (b là số có 1 chữ số ,A có nhiều hơn 1 chữ số)
=> A + 1808 = Ab
=> A + 1808 = 10A +b
=> 9A = 1809 - (b+1)
ta có 1809 chia hết cho 9 => b+1 chia hết cho 9
mà 0 <b <10 => 1<b+1<11
=> b+1 =9 => b=8
=> 9A= 1809 -9
=> A= 200
=> số phải tìm là 2008

-space: normal; widows: 2; word-spacinSố thứ nhất không thể nhiều hơn 4 chữ số vì tổng 4 số bằng 2003. Nếu số thứ
nhất có ít hơn 4 chữ số thì sẽ không tồn tại số thứ tư. Vậy số thứ nhất phải có 4 chữ số.
Gọi số thứ nhất là abcd (a > 0, a, b, c, d < 10). Số thứ hai, số thứ ba, số thứ tư lần lượt sẽ
là : abc ; ab ; a. Theo bài ra ta có phép tính :
abcd + abc + ab + a = 2003.
Theo phân tích cấu tạo số ta có : aaaa + bbb + cc + d = 2003 (*)
Từ phép tính (*) ta có a < 2, nên a = 1. Thay a = 1 vào (*) ta được :
1111 + bbb + cc + d = 2003.
bbb + cc + d = 2003 - 1111
bbb + cc + d = 892 (**)
b > 7 vì nếu b nhỏ hơn hoặc bằng 7 thì bbb + cc + d nhỏ hơn 892 ; b < 9 vì nếu b = 9 thì
bbb = 999 > 892. Suy ra b chỉ có thể bằng 8.
Thay b = 8 vào (**) ta được :
888 + cc + d = 892
cc + d = 892 - 888
cc + d = 4
Từ đây suy ra c chỉ có thể bằng 0 và d = 4.
Vậy số thứ nhất là 1804, số thứ hai là 180, số thứ ba là 18 và số thứ tư là 1.
Số thứ nhất không thể nhiều hơn 4 chữ số vì tổng 4 số bằng 2003. Nếu số thứ
nhất có ít hơn 4 chữ số thì sẽ không tồn tại số thứ tư. Vậy số thứ nhất phải có 4 chữ số.
Gọi số thứ nhất là abcd (a > 0, a, b, c, d < 10). Số thứ hai, số thứ ba, số thứ tư lần lượt sẽ
là : abc ; ab ; a. Theo bài ra ta có phép tính :
abcd + abc + ab + a = 2003.
Theo phân tích cấu tạo số ta có : aaaa + bbb + cc + d = 2003 (*)
Từ phép tính (*) ta có a < 2, nên a = 1. Thay a = 1 vào (*) ta được :
1111 + bbb + cc + d = 2003.
bbb + cc + d = 2003 - 1111
bbb + cc + d = 892 (**)
b > 7 vì nếu b nhỏ hơn hoặc bằng 7 thì bbb + cc + d nhỏ hơn 892 ; b < 9 vì nếu b = 9 thì
bbb = 999 > 892. Suy ra b chỉ có thể bằng 8.
Thay b = 8 vào (**) ta được :
888 + cc + d = 892
cc + d = 892 - 888
cc + d = 4
Từ đây suy ra c chỉ có thể bằng 0 và d = 4.
Vậy số thứ nhất là 1804, số thứ hai là 180, số thứ ba là 18 và số thứ tư là 1.
Thử lại : 1804 + 180 + 18 + 1 = 2003 (đúng)

Bài 1:
a) \(A=\left\{51;62;73;84;95;40\right\}\)
b) \(B=\left\{21;63;84;42\right\}\)
c) \(C=\left\{17;26;35\right\}\)
Bài 2:
a) Số lượng số hạng của dãy số:
\(\left(229-100\right):3+1=44\) (số hạng)
b) Ta có dãy số là: \(10;12;14;16;18;...;98\)
Số lượng số hạng:
\((98-10):2+1=45 \) (số hạng)
Tổng là:
\(\left(98+10\right)\cdot45:2=2430\)
Bài 2:
a) Số lượng số hạng của dãy số:
(229−100):3+1=44(229−100):3+1=44 (số hạng)
b) Ta có dãy số là: 10;12;14;16;18;...;9810;12;14;16;18;...;98
Số lượng số hạng:
(98−10):2+1=45(98−10):2+1=45 (số hạng)
Tổng là:
(98+10)⋅45:2=2430
chỉ làm đc bài 2 thoi

3^1001.7^1002.13^1003
=3^1000.3.7^1000.7^2.13^1000.13^3
=(3^4)^250.(7^4)^250.(13^4)^250.3.49. ......7
=...1 . ...1 . ....1 . 3 . 49 . ...7
=...9
Vậy chữ số hàng đơn vị là 9




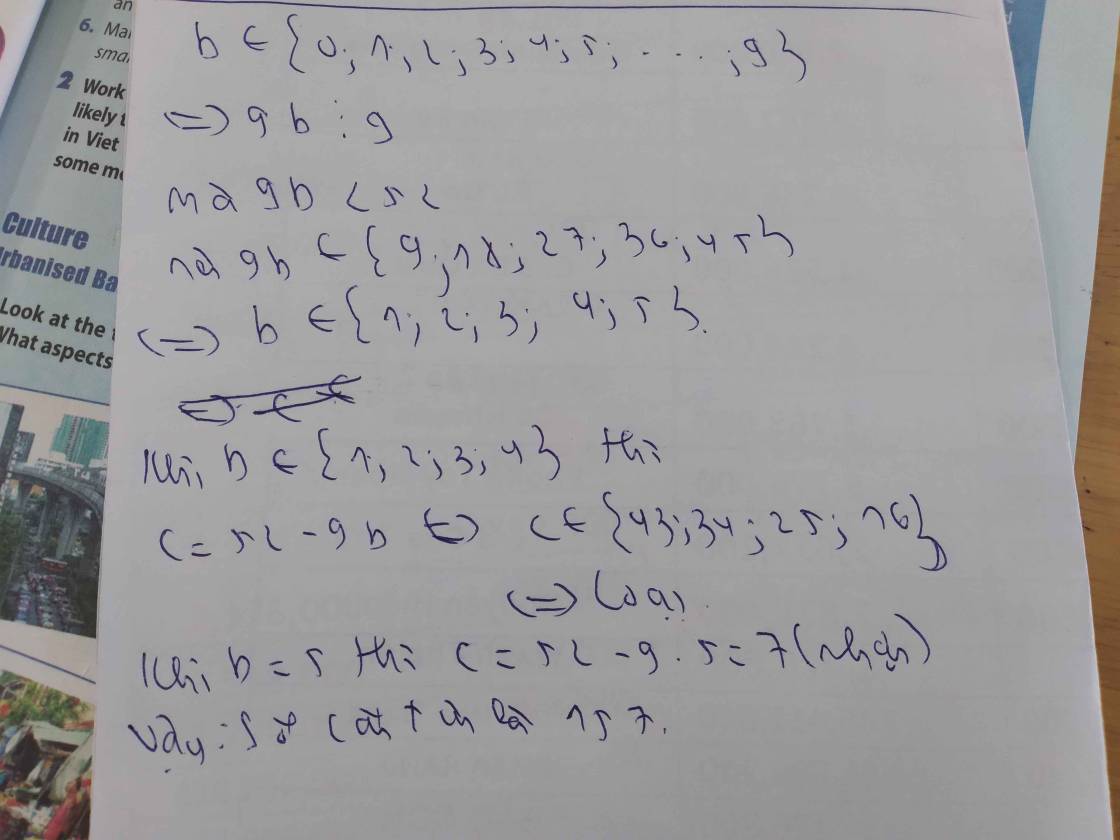
tận cùng của B là 4