So sánh:\(x^2\)\(và\)\(x\)\(biết:x\inℚ\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng tính chất của dãy tỉ số bằng nhau, có:
\(\frac{x}{2}=\frac{y}{3}=\frac{x+y}{2+3}=\frac{20}{5}=4\)
Suy ra: \(\frac{x}{2}=4\Rightarrow x=4\cdot2=8\)
\(\frac{y}{3}=4\Rightarrow y=3\cdot4=12\)

Vì x : 1,2 = y : 0,4 nên \(\frac{x}{{1,2}} = \frac{y}{{0,4}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{{1,2}} = \frac{y}{{0,4}} = \frac{{x - y}}{{1,2 - 0,4}} = \frac{2}{{0,8}} = 2,5\)
Vậy x = 1,2 . 2,5 = 3; y = 0,4 . 2,5 = 1

Ta có : `x/5=y/3` và `x-y=-2`
ADTC dãy tỉ số bằng nhau ta có :
`x/5 = y/3 =(x-y)/(5-3)=(-2)/2=-1`
`=>x/5=-1=>x=-1.5=-5`
`=>y/3=-1=>y=-1.3=-3`
Vậy `x=-5;y=-3`
Áp dụng tính chất của DTSBN, ta được:
x/5=y/3=(x-y)/(5-3)=-2/2=-1
=>x=-5; y=-3

ta xét 3 TH
TH1 x < -2
=> x+2 < 0 và x-2 < 0
=> | x + 2 | + | x - 2 | = -x - 2 + 2 - x = -2x = 4 => x = 2 (loại)
TH2 -2 < x < 2
=> x + 2 > 0 và x - 2 < 0
=> | x + 2 | + | x - 2 | = x + 2 + 2 -x = 4 = 4
TH2 này là TH đặc biệt nên mọi x \(\in\)Q mà -2<x<2 đều thỏa mãn (1)
TH3 x > 2
=> x + 2 > 0 và x - 2 < 0
=> | x + 2 | + | x - 2 | = x + 2 + x - 2 = 2x = 4 => x = 2 (t/m) (2)
kết hợp giữa 1 và 2 ta có với mọi x mà -2 < x < 2 \(x\in Q\)thì đều thỏa mãn

\(\frac{x}{y}=\frac{21}{2}\Rightarrow\frac{x}{21}=\frac{y}{2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{x}{12}=\frac{y}{2}=\frac{x+y}{12+2}=\frac{63}{14}=4.5\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{12}=4.5\rightarrow x=4.5\cdot12=54\\\frac{y}{2}=4.5\rightarrow y=4.5\cdot2=9\end{cases}}\)
\(\frac{x}{y}=\frac{21}{2}\)
\(\frac{x}{21}=\frac{y}{2}\)
Ta có
\(\frac{x}{12}=\frac{y}{2}=\frac{x+y}{12+2}=\frac{63}{14}=4.5\)
Đến đây ta chia 2 trường hợp rồi bn tự kết luận nhé !!!
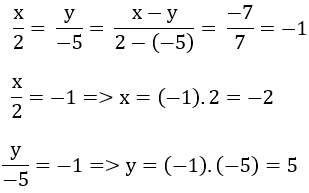
ko hiểu
so sánh:x^2 và x biết như trên